In this post, I will examine Dynamic Linear Models and Time-Series Regression. I will return to data for Engineers from Statistics Sweden. Since the salaries for each year, each stratum (age group) is strongly correlated with the salary for the previous year it does not seem too distant to use a time series to represent the change of salaries throughout the period.
I will let the age represent the season in the time series. This violates the properties of a regular time series and has to be considered for the rest of the analysis. First, let´s decompose the series into its trend and seasonal patterns.
First, define libraries and functions.
library (tidyverse)
## -- Attaching packages --------------------------------------- tidyverse 1.3.1 --
## v ggplot2 3.3.3 v purrr 0.3.4
## v tibble 3.1.0 v dplyr 1.0.5
## v tidyr 1.1.3 v stringr 1.4.0
## v readr 1.4.0 v forcats 0.5.1
## Warning: package 'ggplot2' was built under R version 4.0.3
## Warning: package 'tibble' was built under R version 4.0.5
## Warning: package 'tidyr' was built under R version 4.0.5
## Warning: package 'readr' was built under R version 4.0.3
## Warning: package 'dplyr' was built under R version 4.0.5
## Warning: package 'forcats' was built under R version 4.0.3
## -- Conflicts ------------------------------------------ tidyverse_conflicts() --
## x dplyr::filter() masks stats::filter()
## x dplyr::lag() masks stats::lag()
library(imputeTS)
## Warning: package 'imputeTS' was built under R version 4.0.5
## Registered S3 method overwritten by 'quantmod':
## method from
## as.zoo.data.frame zoo
library(TSstudio)
## Warning: package 'TSstudio' was built under R version 4.0.5
library(forecast)
## Warning: package 'forecast' was built under R version 4.0.5
library(dynlm)
## Warning: package 'dynlm' was built under R version 4.0.5
## Loading required package: zoo
## Warning: package 'zoo' was built under R version 4.0.5
##
## Attaching package: 'zoo'
## The following object is masked from 'package:imputeTS':
##
## na.locf
## The following objects are masked from 'package:base':
##
## as.Date, as.Date.numeric
library(lmtest)
## Warning: package 'lmtest' was built under R version 4.0.4
library(sandwich)
## Warning: package 'sandwich' was built under R version 4.0.3
library(ggeffects)
## Warning: package 'ggeffects' was built under R version 4.0.5
readfile <- function (file1){
read_csv (file1, col_types = cols(), locale = readr::locale (encoding = "latin1"), na = c("..", "NA")) %>%
gather (starts_with("19"), starts_with("20"), key = "year", value = salary) %>%
mutate (year_n = parse_number (year))
}
# Thanks to Grant, Stack Overflow
predNeweyWest <- function (model){
pred_df <- data.frame(fit = predict(model))
X_mat <- model.matrix(model)
v_hac <- NeweyWest(model, prewhite = FALSE, adjust = TRUE)
var_fit_hac <- rowSums((X_mat %*% v_hac) * X_mat)
se_fit_hac <- sqrt(var_fit_hac)
pred_df <-
pred_df %>%
mutate(se_fit_hac = se_fit_hac) %>%
mutate(
lwr_hac = fit - qt(0.975, df = model$df.residual) * se_fit_hac,
upr_hac = fit + qt(0.975, df = model$df.residual) * se_fit_hac
)
}
plotmodel <- function(data, pred_df, no_n = FALSE){
if(no_n){
bind_cols(
data,
pred_df
) %>%
ggplot(aes(x = year_dec, y = salary, ymin = lwr_hac, ymax = upr_hac)) +
geom_point() +
geom_ribbon(fill = "#E41A1C", alpha = 0.3, col = NA) +
labs(
x = "Year",
y = "Salary (SEK/month)",
caption = 'Shaded region indicates HAC 95% CI.'
)
}
else{
bind_cols(
data,
pred_df
) %>%
ggplot(aes(x = year_dec, y = salary, color = n, ymin = lwr_hac, ymax = upr_hac)) +
geom_point() +
geom_ribbon(fill = "#E41A1C", alpha = 0.3, col = NA) +
labs(
x = "Year",
y = "Salary (SEK/month)",
caption = 'Shaded region indicates HAC 95% CI.'
)
}
}
assess_model <- function(model, timeseries, data, no_n = FALSE, doexp = FALSE){
print(summary (model))
print(coeftest(model, vcov = NeweyWest, prewhite = F, adjust = T))
print(checkresiduals(model))
if(doexp){
pred_df <- exp(predNeweyWest(model))
} else {
pred_df <- predNeweyWest(model)
}
pred_df$year_dec <- timeseries
plotmodel(data, pred_df, no_n)
}The data table is downloaded from Statistics Sweden. It is saved as a comma-delimited file without heading, 000000D2_20210506-201343.csv, http://www.statistikdatabasen.scb.se/pxweb/en/ssd/.
The table: Average monthly pay (total pay), non-manual workers all sectors (SLP), SEK by occupational group (SSYK), age, sex and year. SSYK 2012 214, Year 2014 - 2019
The average age within each age group is used as a numeric value for graphical presentation and the linear model.
The number of Engineers in each stratum is downloaded separately in the file 000000CZ_20210506-201420.csv.
tb <- readfile("000000D2_20210506-201343.csv") %>%
rowwise() %>%
mutate(age_l = unlist(lapply(strsplit(substr(age, 1, 5), "-"), strtoi))[1]) %>%
rowwise() %>%
mutate(age_h = unlist(lapply(strsplit(substr(age, 1, 5), "-"), strtoi))[2]) %>%
mutate(age_n = (age_l + age_h) / 2)
tbcount <- readfile("000000CZ_20210506-201420.csv")
tbcount$salary <- replace(tbcount$salary, is.na(tbcount$salary), 0)
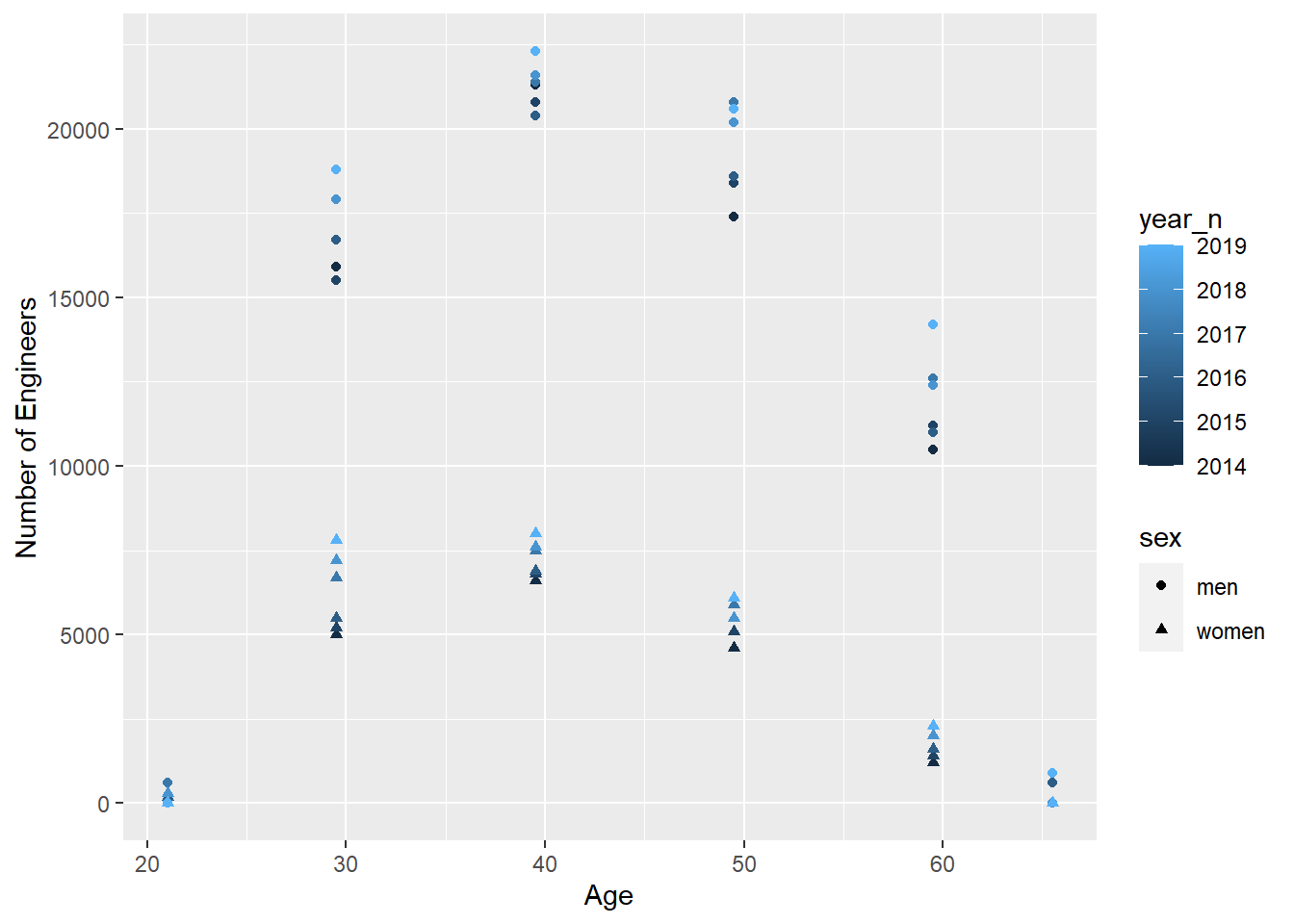
tb$n <- tbcount$salaryLet’s have a look at the age distribution for the different years for men and women.
tb %>%
ggplot () +
geom_point (mapping = aes(x = age_n,y = n, colour = year_n, shape = sex)) +
labs(
x = "Age",
y = "Number of Engineers"
)
Create a time series for each gender. Time series can not have missing values, Impute missing values in time series with arima model. Women don’t have any data for the age group 65-66 year, that group is filtered away.
tb_men <- filter(tb, sex == "men")
tb_women <- filter(tb, sex == "women") %>% filter(age_n != 65.5)
summary(tb_men$salary)
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## 27300 36550 47100 43340 49500 52800 1
summary(tb_women$salary)
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## 26600 35000 44700 41293 45900 52100 1
tbts_men <- ts(tb_men$salary, start = 2014, freq = 6) %>% na_kalman("auto.arima")
tbts_women <- ts(tb_women$salary, start = 2014, freq = 5) %>% na_kalman("auto.arima")
tb_men$salary <- as.numeric(tbts_men)
tb_women$salary <- as.numeric(tbts_women)Let’s use the decompose function from the stats package to view the trend, seasonal and random component of the time series.
decompose(tbts_men) %>% plot()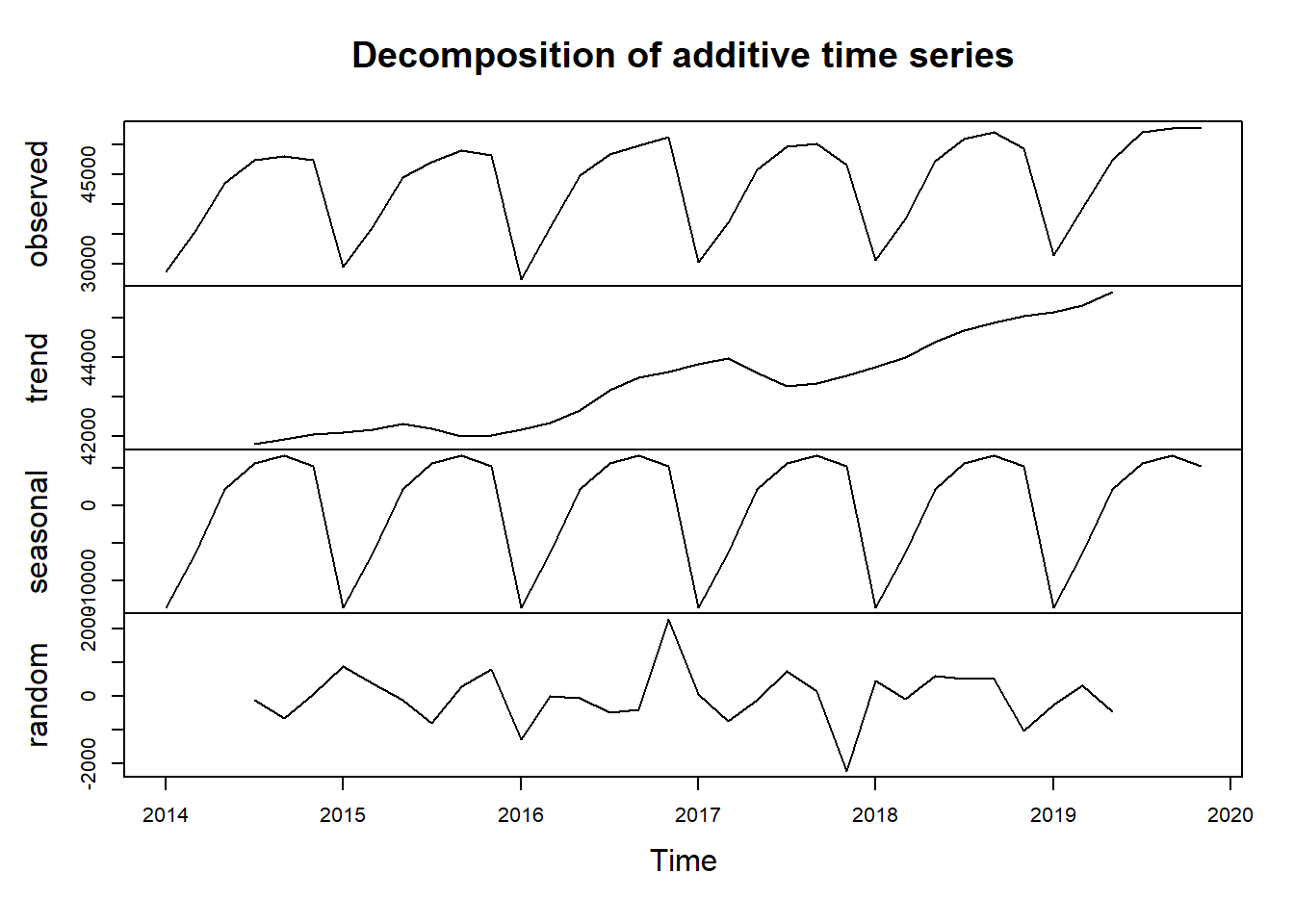
decompose(tbts_women) %>% plot()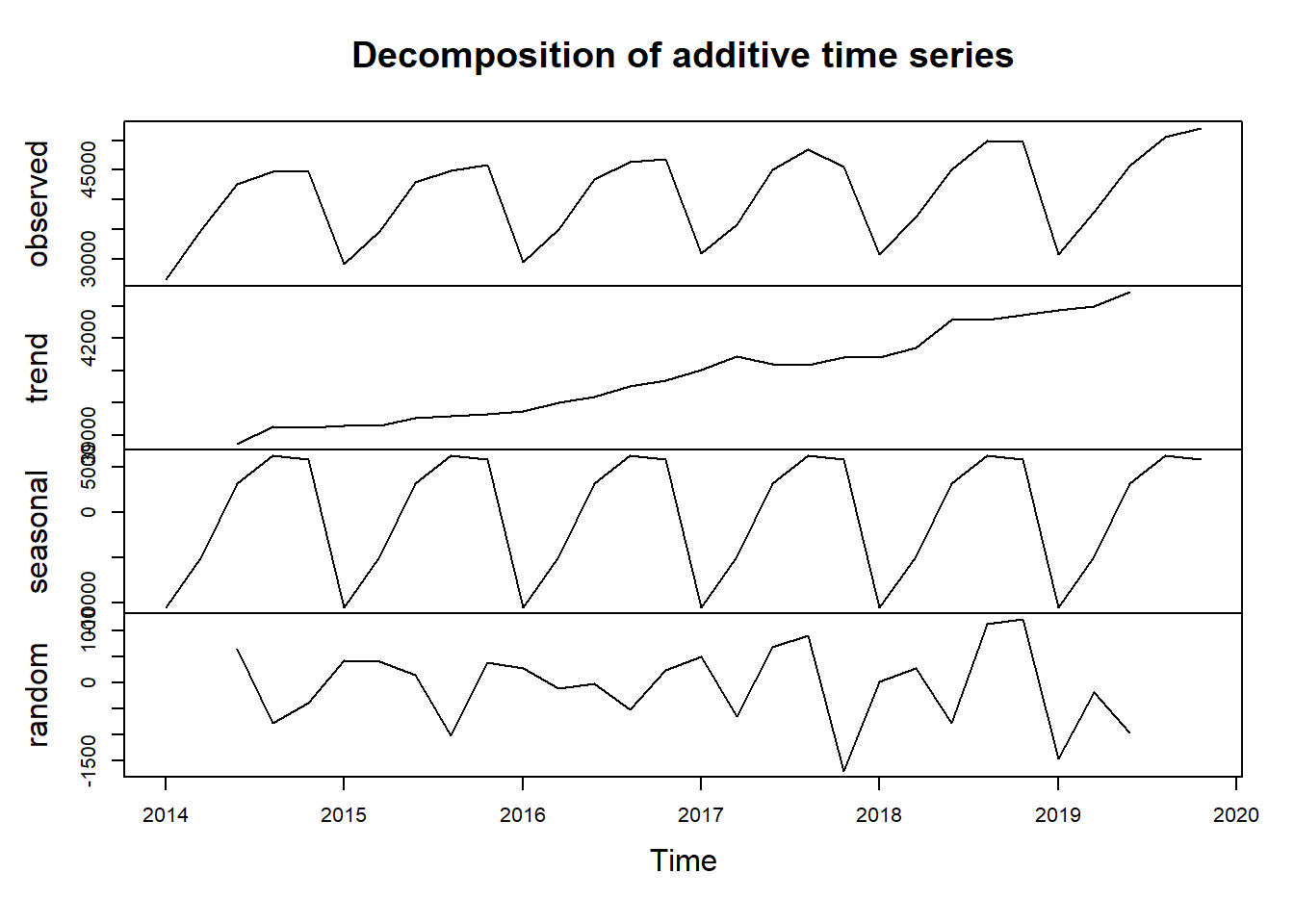
Let´s have a look at the autocorrelation for the series. As expected the series for men shows a strong correlation with its sixth lag, i.e. the same age category the year before. The series for women shows a strong correlation with its fifth lag.
acf(tbts_men, 36)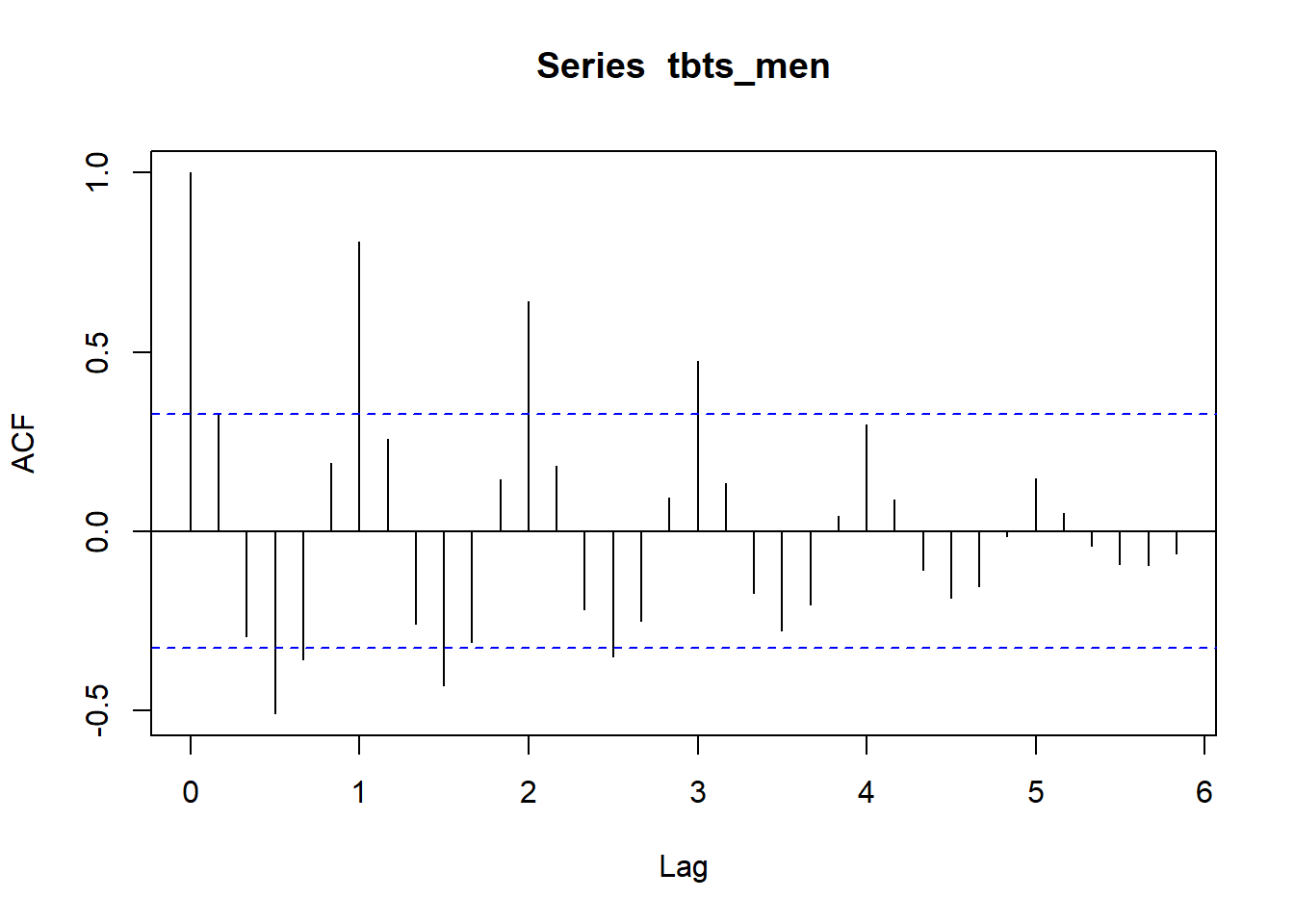
acf(tbts_women, 30)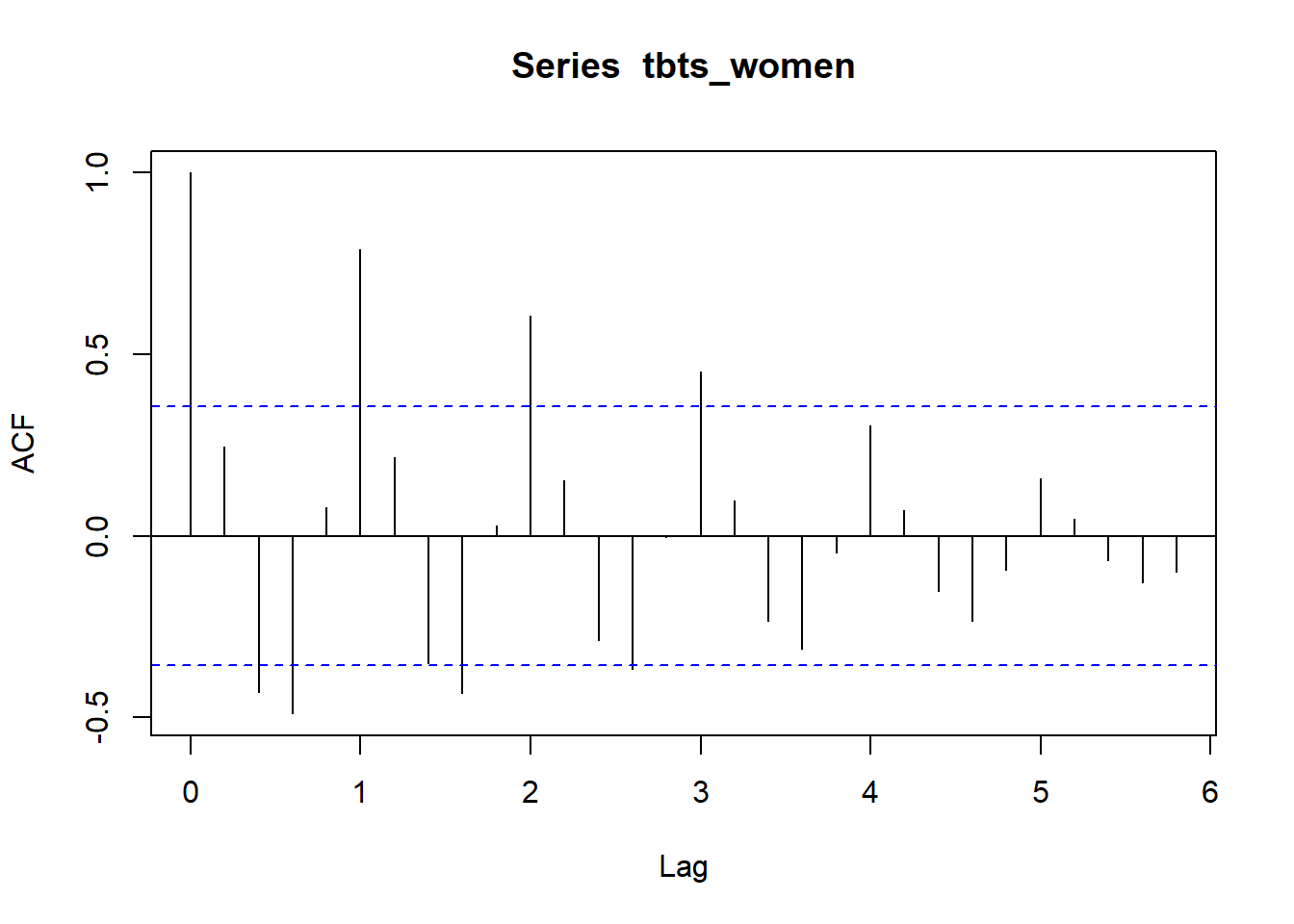
The partial autocorrelation function gives the partial correlation of a stationary time series with its own lagged values, regressed the values of the time series at all shorter lags.
pacf(tbts_men, 36)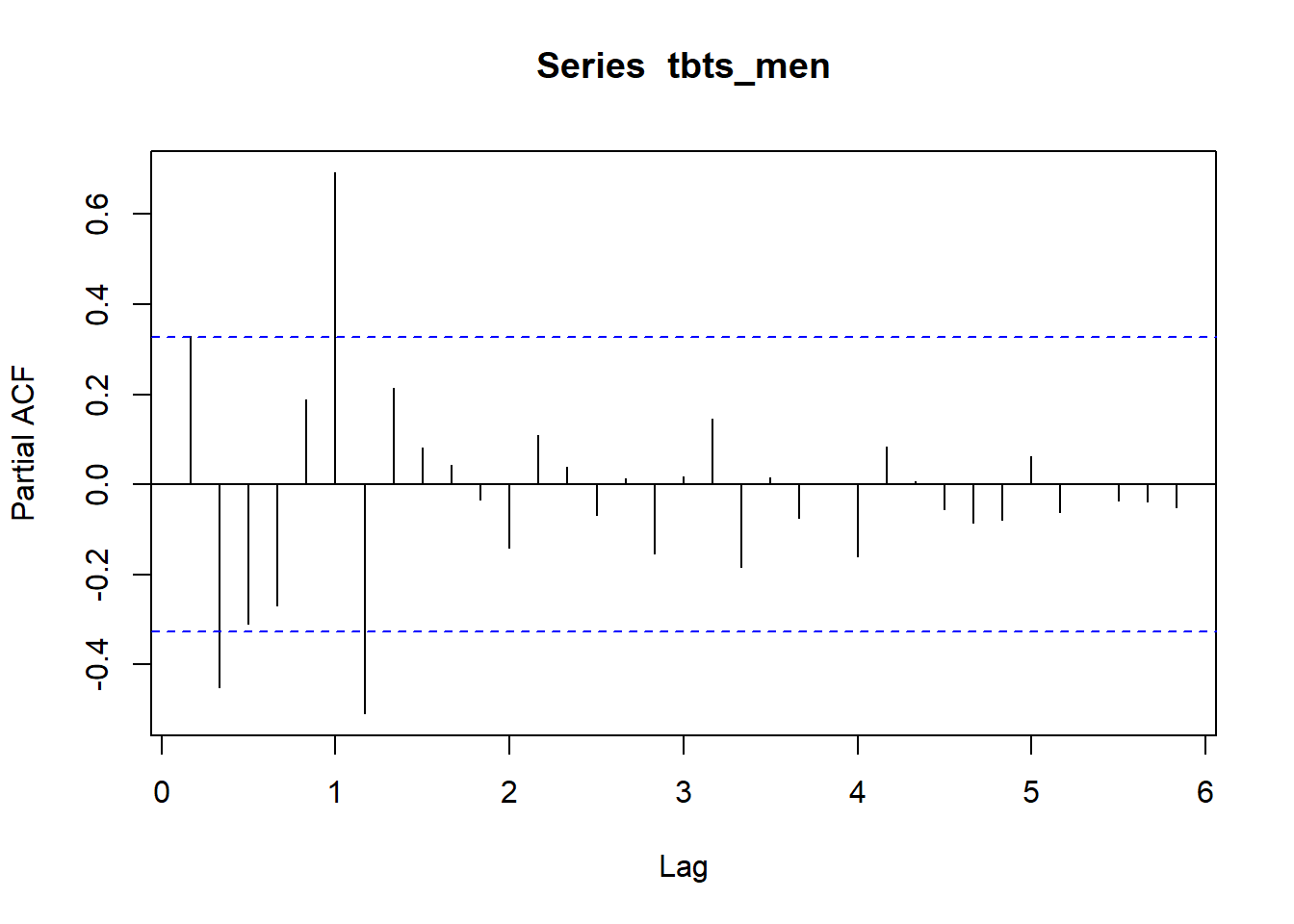
pacf(tbts_women, 36)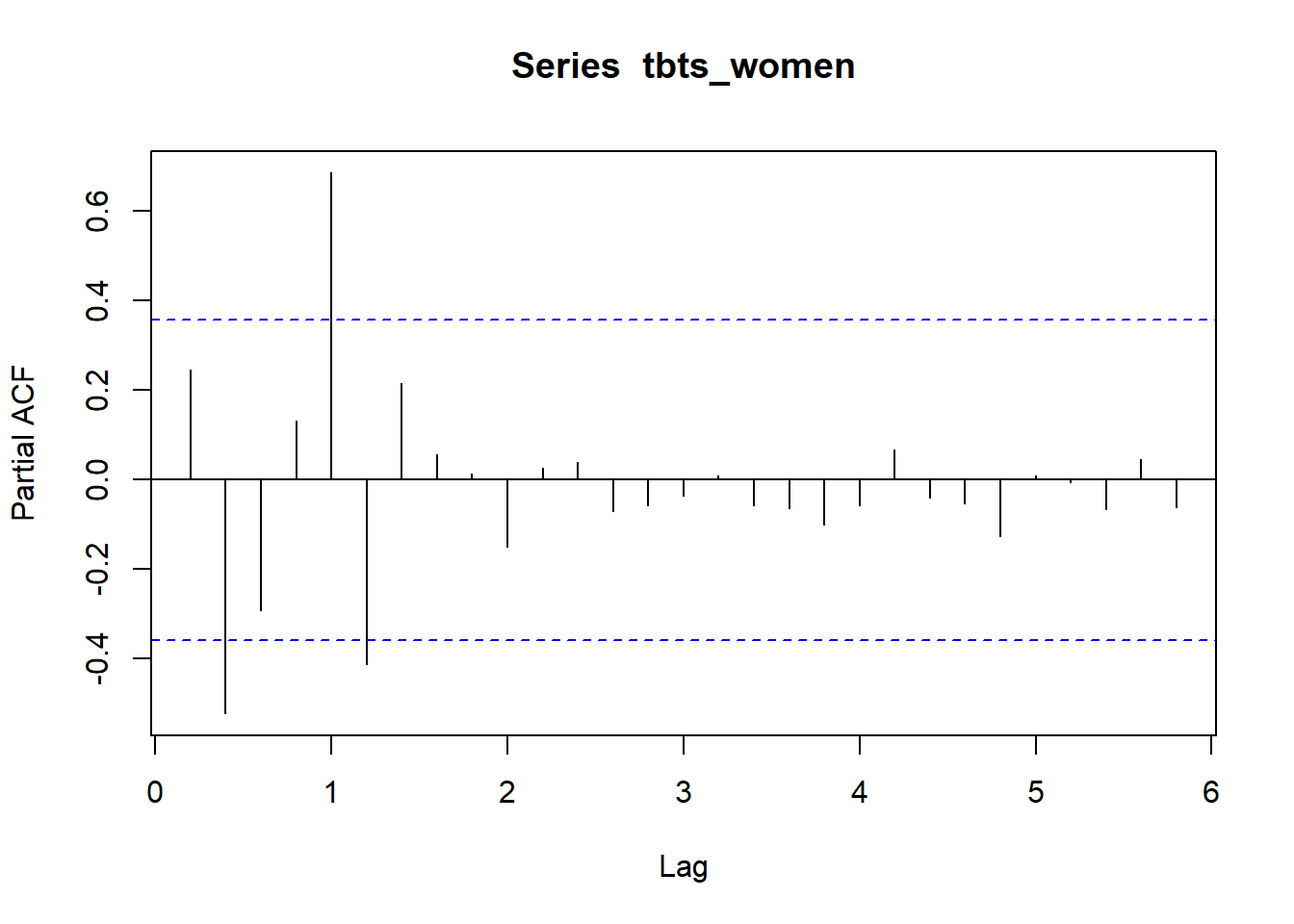
The following plot shows the correlation between the salary and its yearly lag for three years.
ts_lags(tbts_men, c(6, 12, 18))Now, let’s fit an arima model to the time series with the auto.arima from the forecast library. The summary shows that the auto.arima has identified a SAR(2) process with drift and additionally an element of random walk. The checkresiduals function plots the residuals from the arima model, the autocorrelation of the residuals and a histogram of the residual distribution. The Ljung-Box test suggests that only white noise remains in the residual. The ggseasonplot plots the salary distribution on age for the years 2014-2019, remember that we used age as a season in this approach.
arimamodel_men <- auto.arima(tbts_men)
summary(arimamodel_men)
## Series: tbts_men
## ARIMA(0,0,0)(2,1,0)[6] with drift
##
## Coefficients:
## sar1 sar2 drift
## -0.761 -0.6098 128.8569
## s.e. 0.158 0.1435 16.1691
##
## sigma^2 estimated as 1163963: log likelihood=-254.04
## AIC=516.08 AICc=517.68 BIC=521.69
##
## Training set error measures:
## ME RMSE MAE MPE MAPE MASE ACF1
## Training set -25.68999 934.3299 573.1137 -0.1985635 1.37638 0.434177 0.2314468
checkresiduals(arimamodel_men)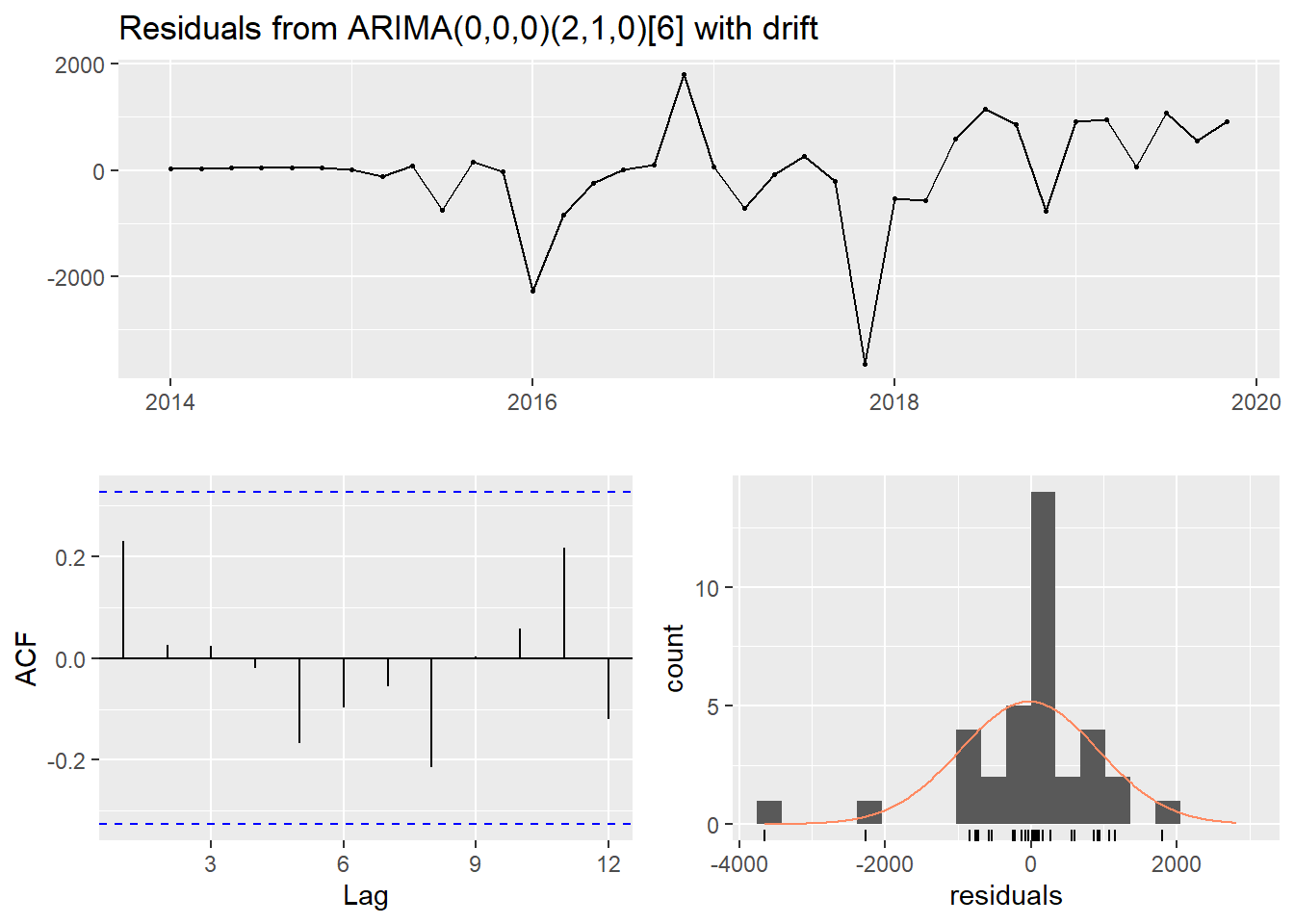
##
## Ljung-Box test
##
## data: Residuals from ARIMA(0,0,0)(2,1,0)[6] with drift
## Q* = 3.9755, df = 4, p-value = 0.4093
##
## Model df: 3. Total lags used: 7
ggseasonplot(tbts_men)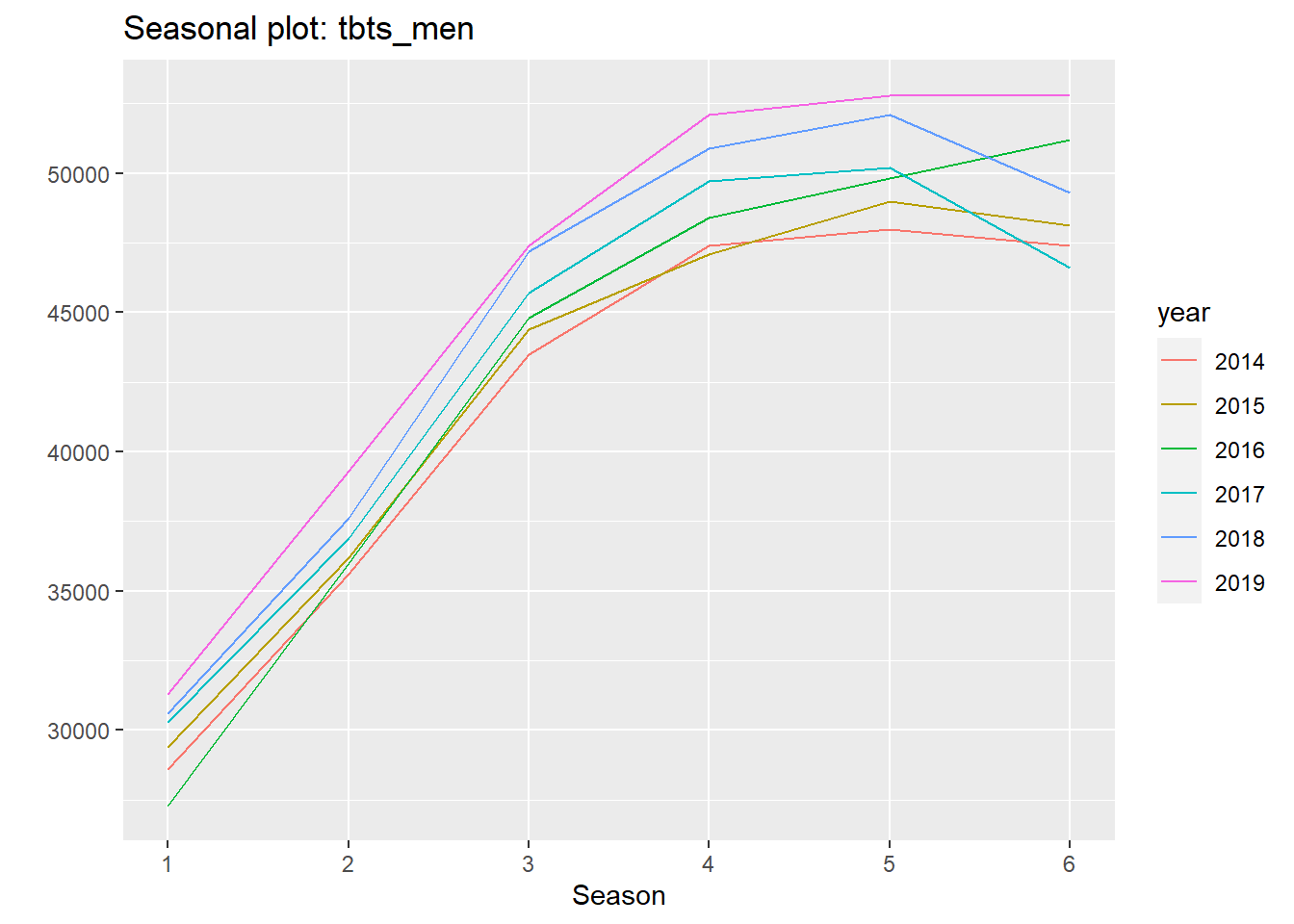
For women, the auto.arima is not able to pick up any SAR. The best fit is according to auto.arima is a constant drift.
arimamodel_women <- auto.arima(tbts_women)
summary(arimamodel_women)
## Series: tbts_women
## ARIMA(0,0,0)(0,1,0)[5] with drift
##
## Coefficients:
## drift
## 188.0000
## s.e. 43.5542
##
## sigma^2 estimated as 1235313: log likelihood=-210.3
## AIC=424.59 AICc=425.14 BIC=427.03
##
## Training set error measures:
## ME RMSE MAE MPE MAPE MASE
## Training set 6.362663 994.108 699.696 -0.07692376 1.730501 0.6551461
## ACF1
## Training set -0.07256362
checkresiduals(arimamodel_women)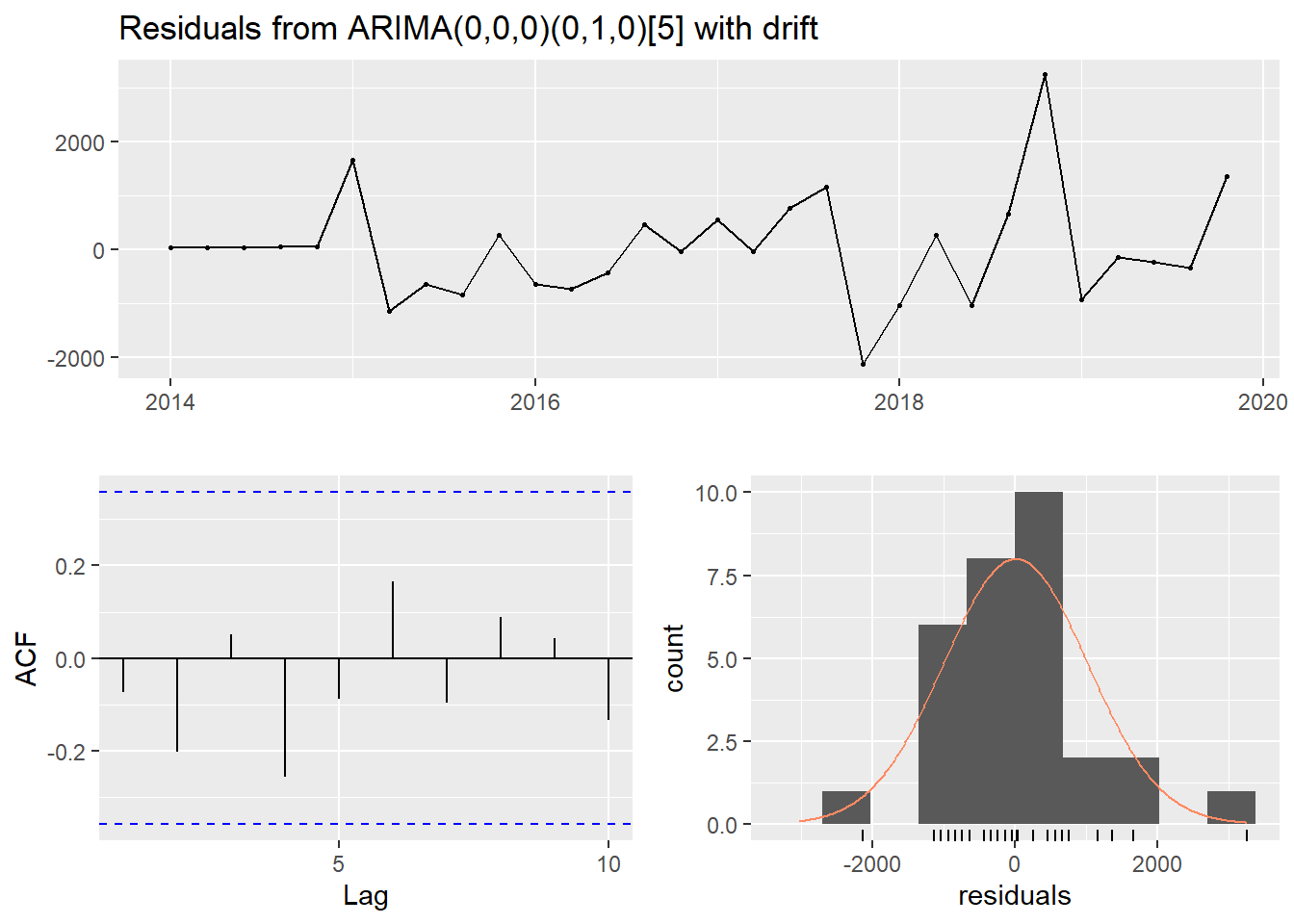
##
## Ljung-Box test
##
## data: Residuals from ARIMA(0,0,0)(0,1,0)[5] with drift
## Q* = 5.4793, df = 5, p-value = 0.3602
##
## Model df: 1. Total lags used: 6
ggseasonplot(tbts_women)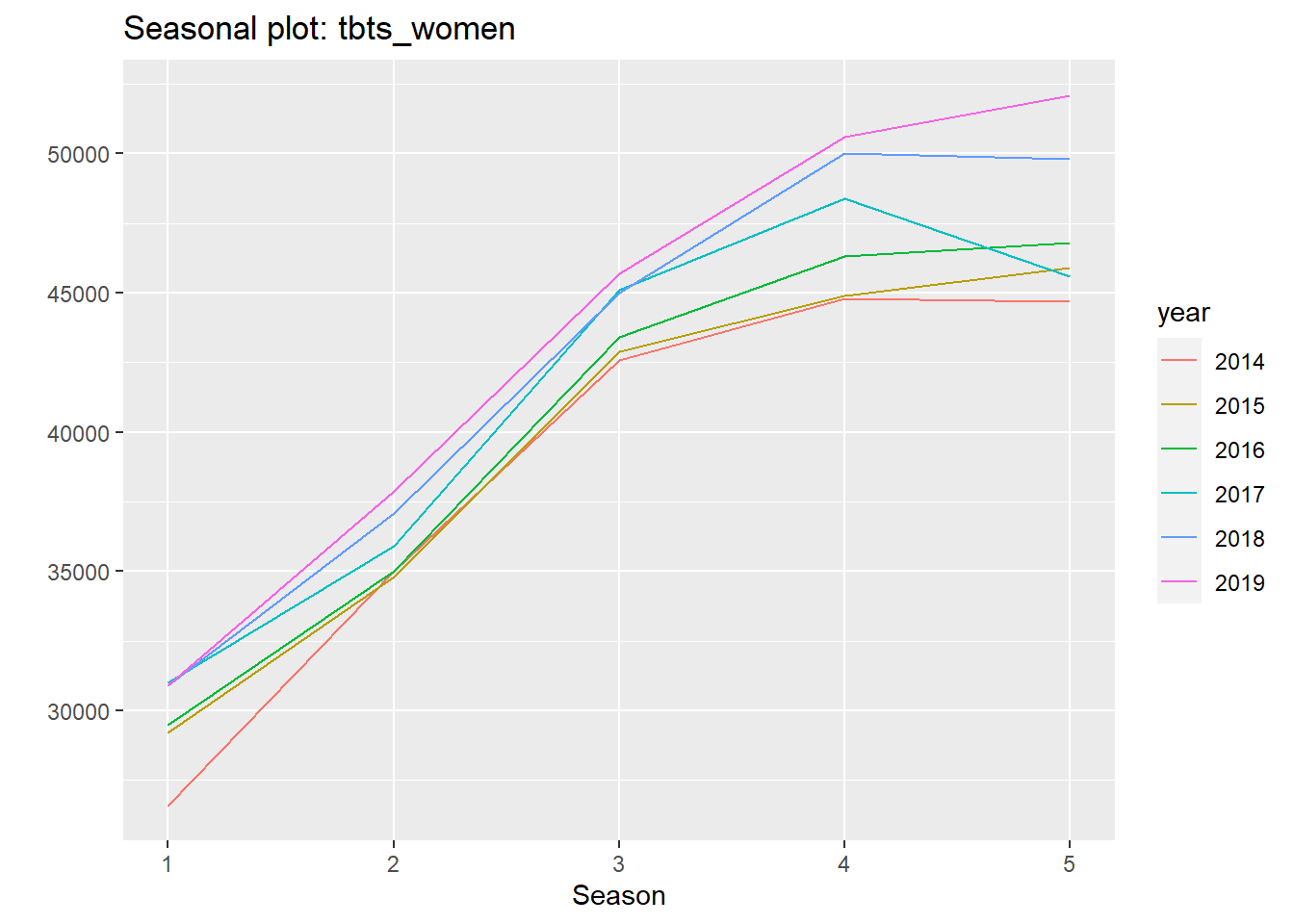
An AR(p) model assumes that a time series Yt can be modelled by a linear function of the first p of its lagged values. Let’s first start to model a seasonal SAR(1) model with the dynlm package. Each year the salaries increase by a fixed amount and a part that is relative to the salary size. I will use the NeweyWest function from the Sandwich package throughout this post to get heteroskedasticity- and autocorrelation-consistent error estimates.
dynmodel_men <- dynlm(ts(salary) ~ L(ts(salary), 6), data = tb_men)
assess_model(dynmodel_men, time(tbts_men)[7:36], tb_men[7:36,], no_n = TRUE)
##
## Time series regression with "ts" data:
## Start = 7, End = 36
##
## Call:
## dynlm(formula = ts(salary) ~ L(ts(salary), 6), data = tb_men)
##
## Residuals:
## Min 1Q Median 3Q Max
## -5517.7 -371.7 48.9 418.0 2600.3
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4.339e+02 1.575e+03 0.275 0.785
## L(ts(salary), 6) 1.009e+00 3.608e-02 27.980 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1522 on 28 degrees of freedom
## Multiple R-squared: 0.9655, Adjusted R-squared: 0.9642
## F-statistic: 782.9 on 1 and 28 DF, p-value: < 2.2e-16
##
##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4.3389e+02 1.8030e+03 0.2406 0.8116
## L(ts(salary), 6) 1.0094e+00 4.3076e-02 23.4340 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Breusch-Godfrey test for serial correlation of order up to 6
##
## data: Residuals
## LM test = 9.8199, df = 6, p-value = 0.1324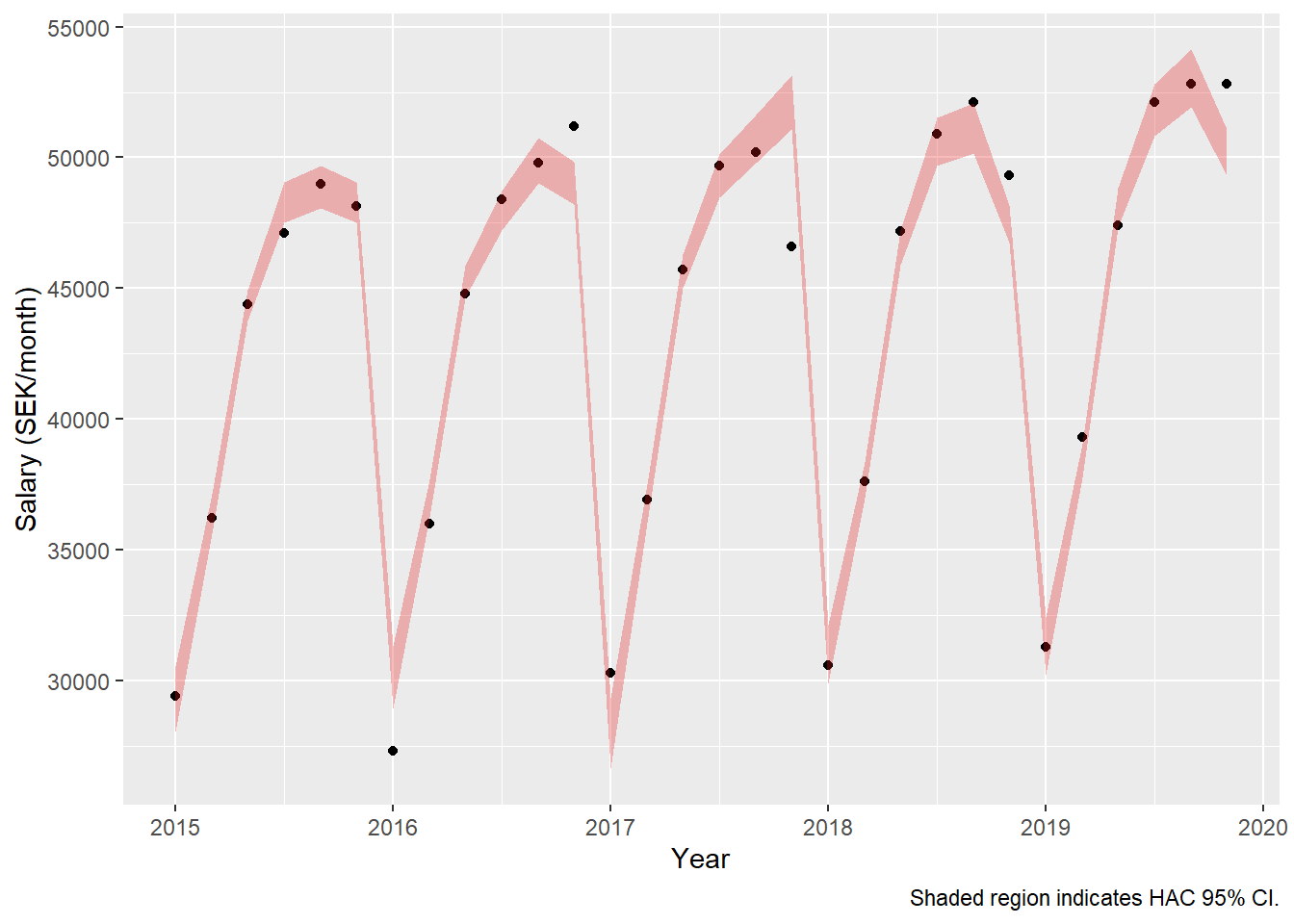
dynmodel_women <- dynlm(ts(salary) ~ L(ts(salary), 5), data = tb_women)
assess_model(dynmodel_women, time(tbts_women)[6:30], tb_women[6:30,], no_n = TRUE)
##
## Time series regression with "ts" data:
## Start = 6, End = 30
##
## Call:
## dynlm(formula = ts(salary) ~ L(ts(salary), 5), data = tb_women)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2266.8 -683.0 -148.9 501.2 3157.1
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.323e+02 1.316e+03 0.101 0.921
## L(ts(salary), 5) 1.020e+00 3.206e-02 31.816 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1126 on 23 degrees of freedom
## Multiple R-squared: 0.9778, Adjusted R-squared: 0.9768
## F-statistic: 1012 on 1 and 23 DF, p-value: < 2.2e-16
##
##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.3234e+02 1.1458e+03 0.1155 0.9091
## L(ts(salary), 5) 1.0200e+00 2.9112e-02 35.0356 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1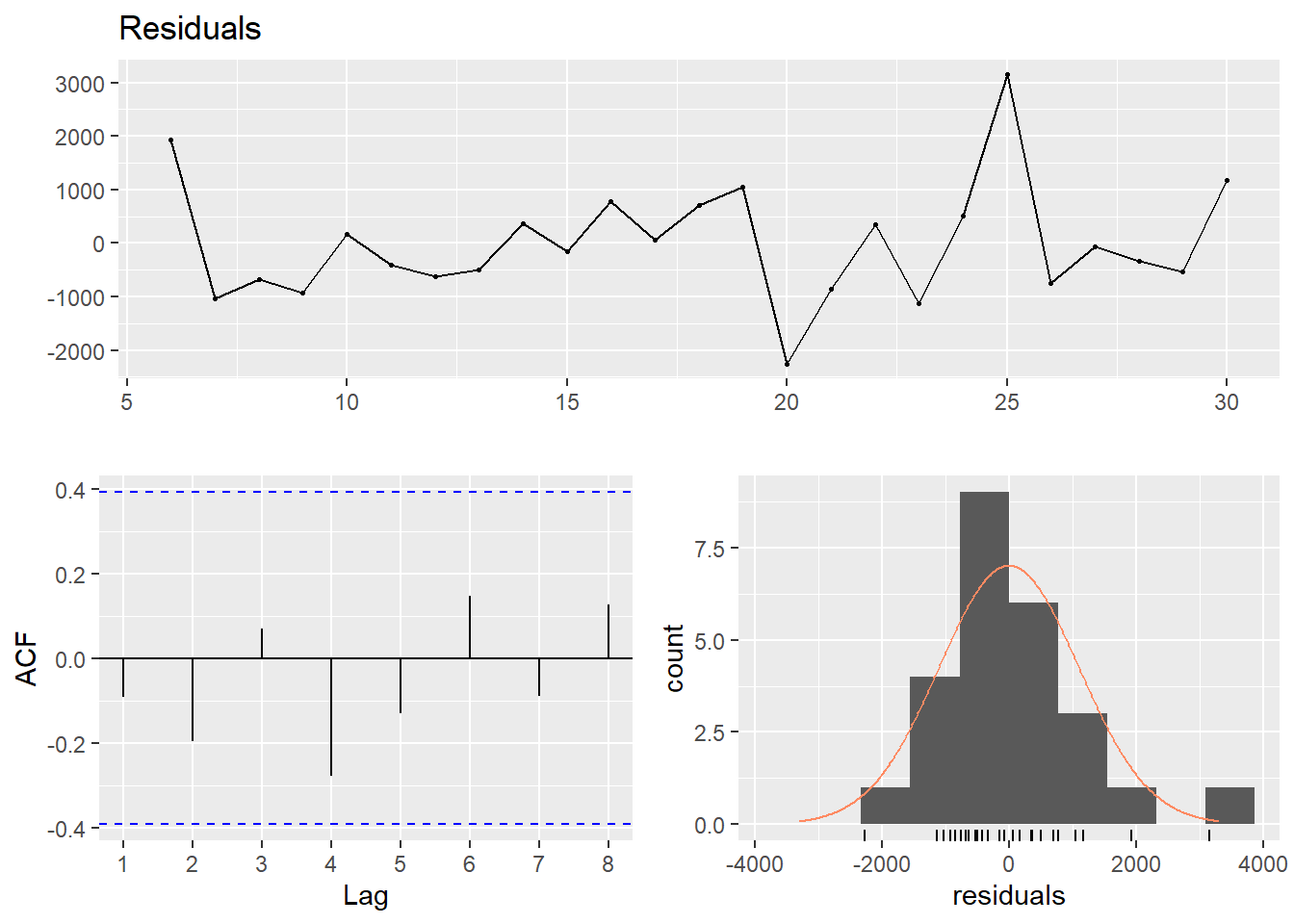
##
## Breusch-Godfrey test for serial correlation of order up to 5
##
## data: Residuals
## LM test = 4.8683, df = 5, p-value = 0.4322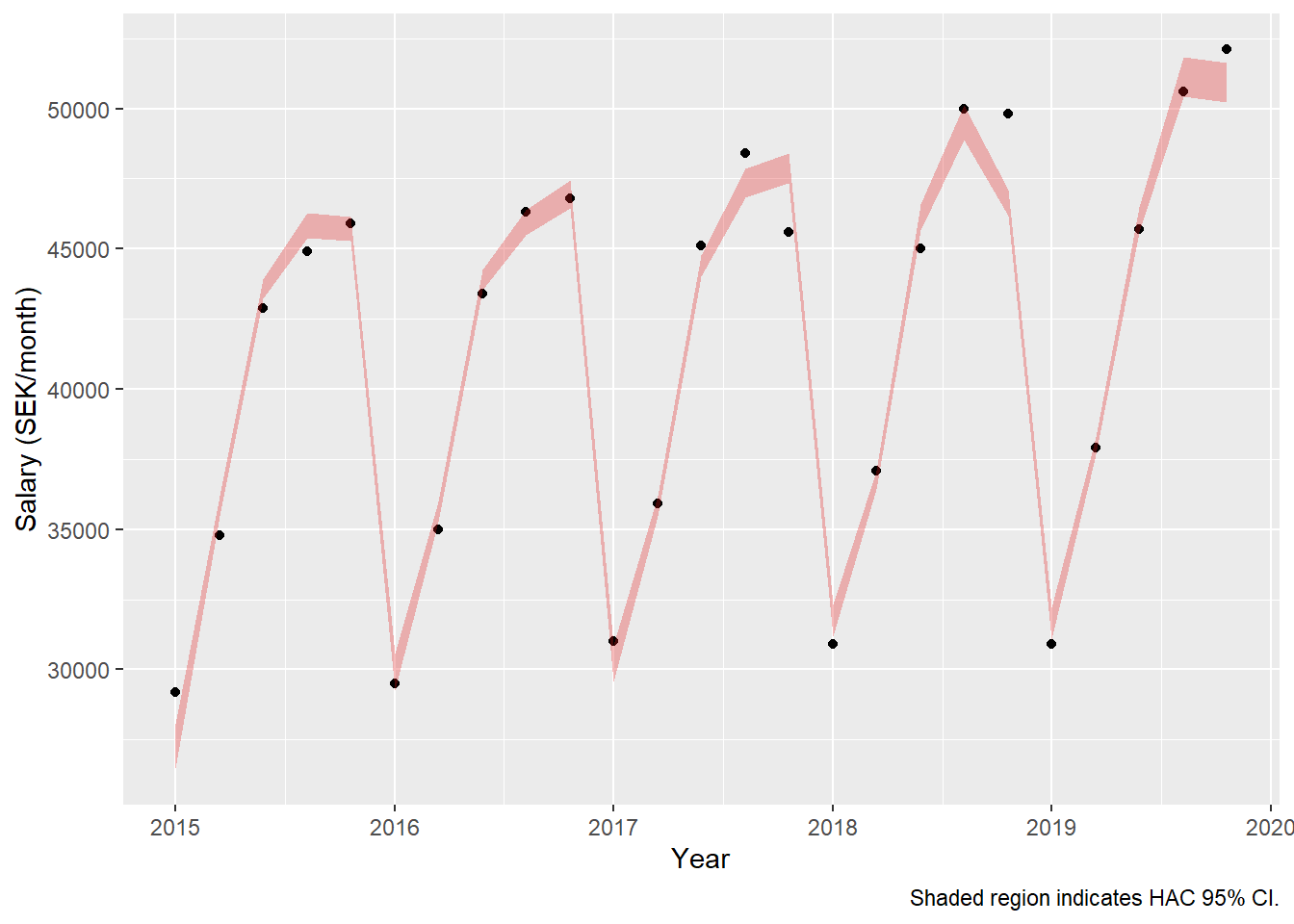
Now also add weights according to the number of engineers in the different strata. Note that the dynamic approach uses the information from the first year to predict the second. Weights from the first year have to be excluded. The fixed amount has decreased from 434 to 134 SEK and the relative part has increased from 0.94 % to 1.6 %. The fixed part is not statistically significant in either of these two models.
dynmodel_men <- dynlm(ts(salary) ~ L(ts(salary), 6), data = tb_men, weights = n[7:36])
assess_model(dynmodel_men, time(tbts_men)[7:36], tb_men[7:36,])
##
## Time series regression with "ts" data:
## Start = 7, End = 36
##
## Call:
## dynlm(formula = ts(salary) ~ L(ts(salary), 6), data = tb_men,
## weights = n[7:36])
##
## Weighted Residuals:
## Min 1Q Median 3Q Max
## -164527 -12301 0 48694 129992
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.343e+02 1.083e+03 0.124 0.902
## L(ts(salary), 6) 1.016e+00 2.398e-02 42.392 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 75460 on 21 degrees of freedom
## Multiple R-squared: 0.9884, Adjusted R-squared: 0.9879
## F-statistic: 1797 on 1 and 21 DF, p-value: < 2.2e-16
##
##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 134.30571 856.80707 0.1568 0.8769
## L(ts(salary), 6) 1.01643 0.01883 53.9780 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1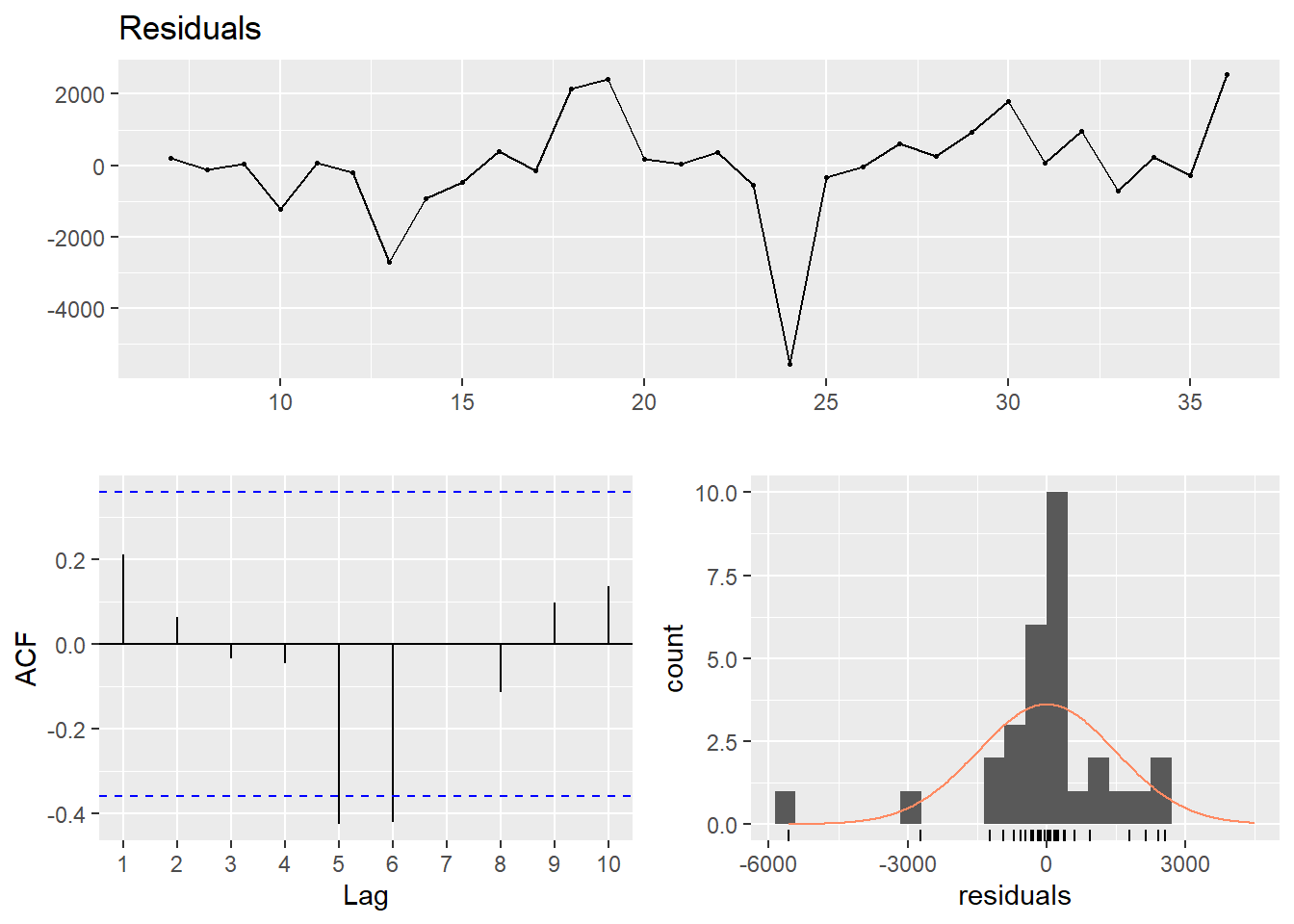
##
## Breusch-Godfrey test for serial correlation of order up to 6
##
## data: Residuals
## LM test = 9.8199, df = 6, p-value = 0.1324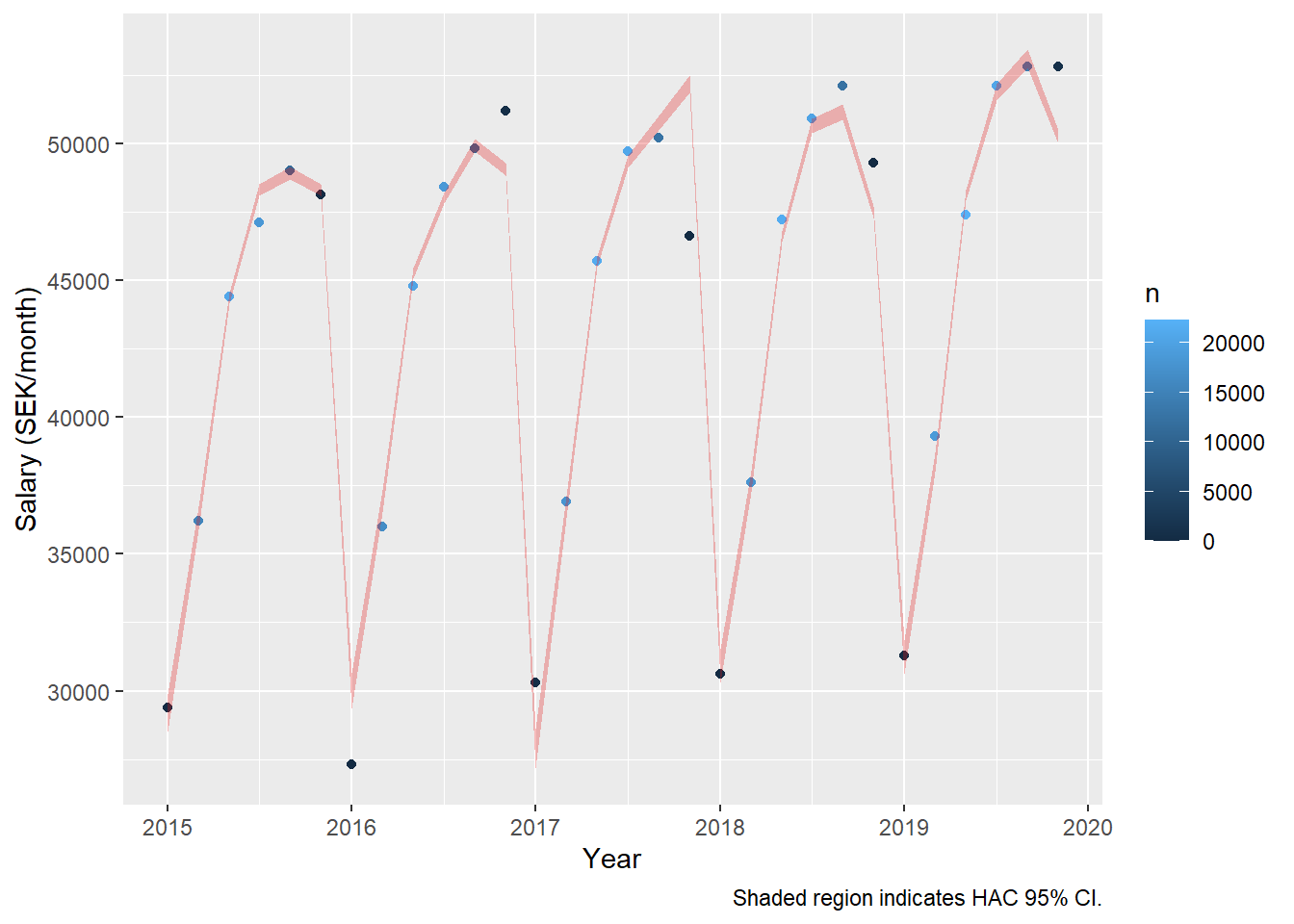
dynmodel_women <- dynlm(ts(salary) ~ L(ts(salary), 5), data = tb_women, weights = n[6:30])
assess_model(dynmodel_women, time(tbts_women)[6:30], tb_women[6:30,])
##
## Time series regression with "ts" data:
## Start = 6, End = 30
##
## Call:
## dynlm(formula = ts(salary) ~ L(ts(salary), 5), data = tb_women,
## weights = n[6:30])
##
## Weighted Residuals:
## Min 1Q Median 3Q Max
## -106359 -30874 0 33627 144325
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -735.01210 1575.94230 -0.466 0.646
## L(ts(salary), 5) 1.03745 0.03693 28.089 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 60090 on 21 degrees of freedom
## Multiple R-squared: 0.9741, Adjusted R-squared: 0.9728
## F-statistic: 789 on 1 and 21 DF, p-value: < 2.2e-16
##
##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -735.012099 708.461714 -1.0375 0.3113
## L(ts(salary), 5) 1.037452 0.014893 69.6602 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1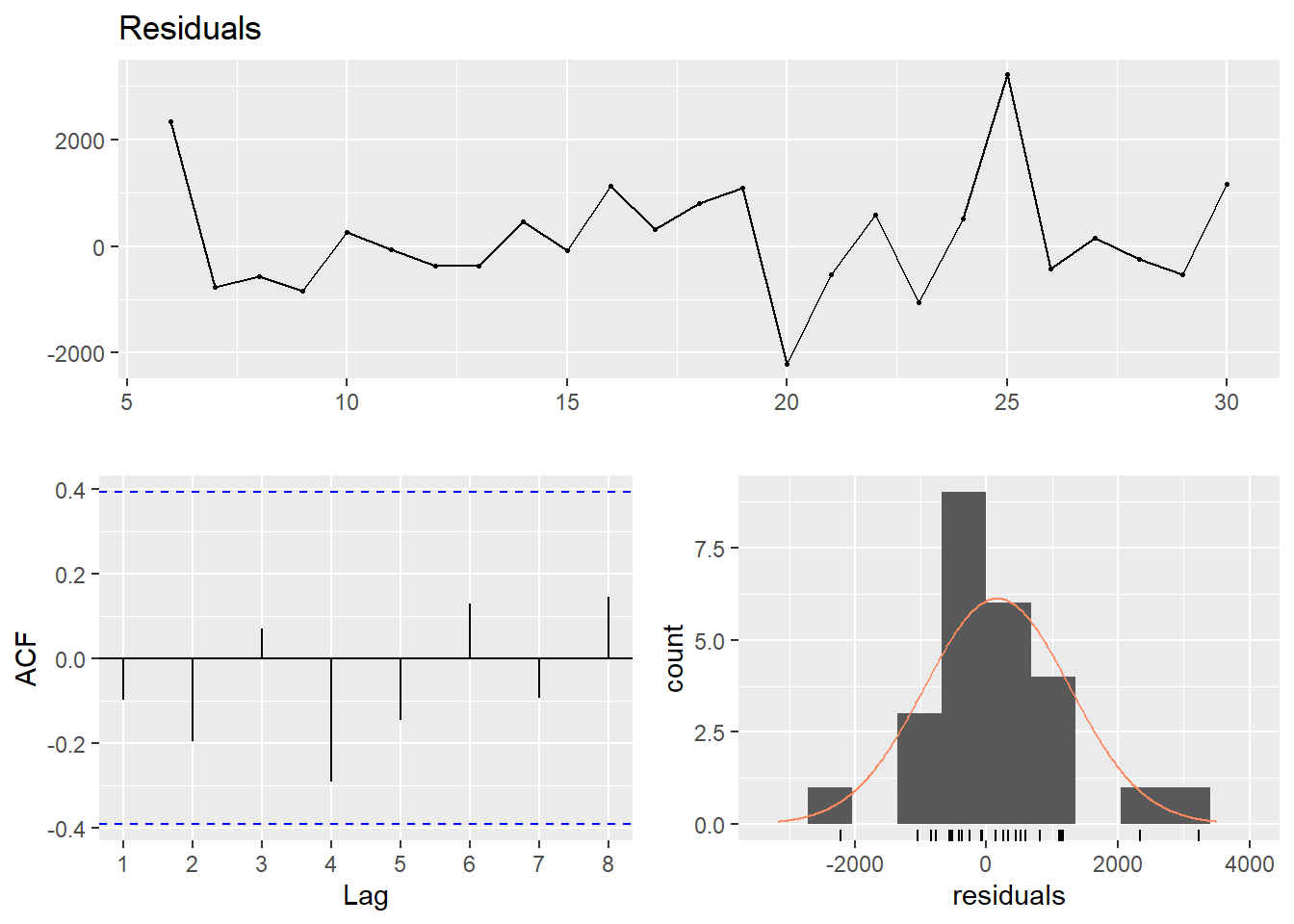
##
## Breusch-Godfrey test for serial correlation of order up to 5
##
## data: Residuals
## LM test = 4.8683, df = 5, p-value = 0.4322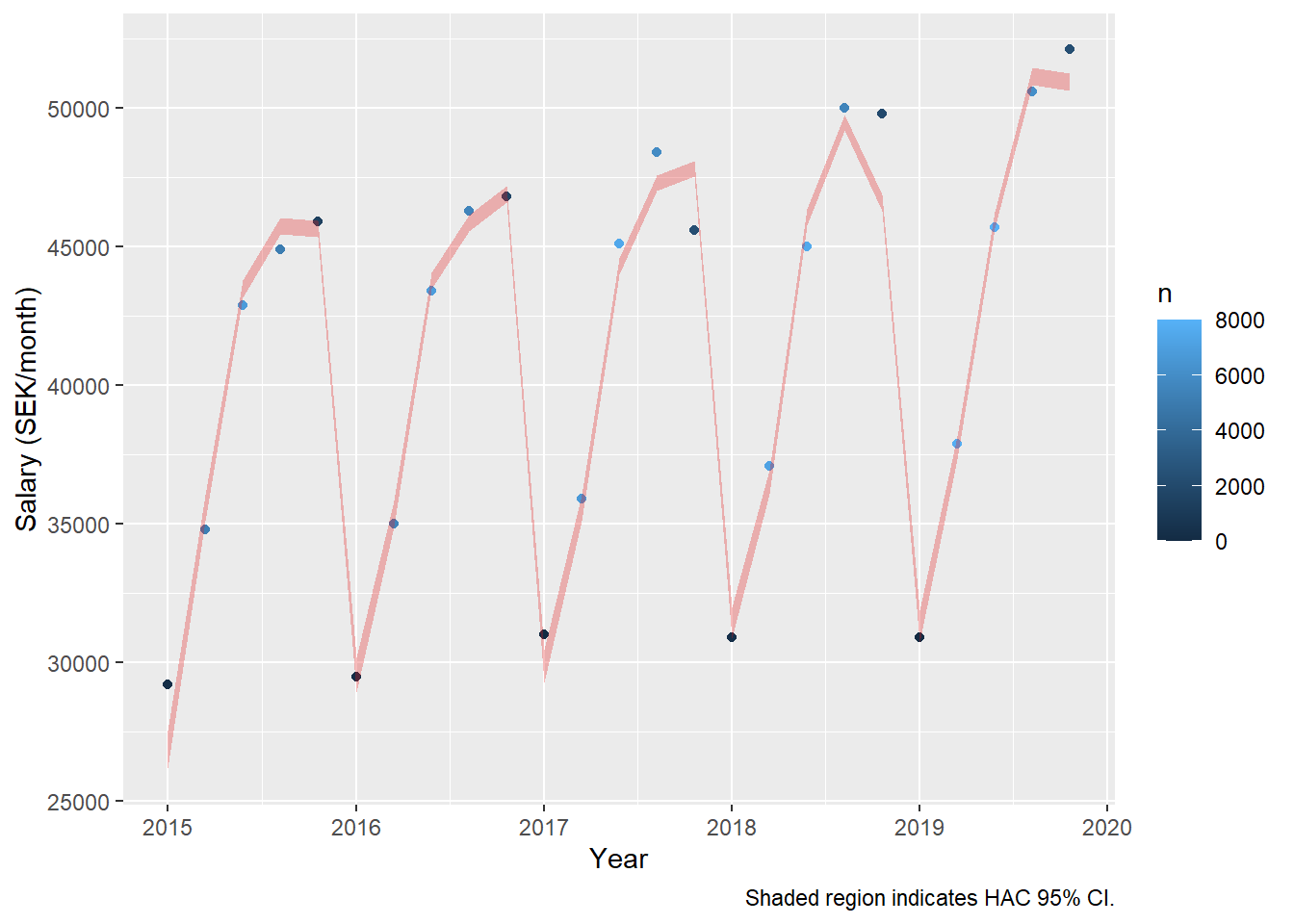
Let’s drop the non-significant intercept. The relative salary raise increases to 1,94 % per year for men and 2,03 % for women.
dynmodel_men <- dynlm(ts(salary) ~ L(ts(salary), 6) - 1, data = tb_men, weights = n[7:36])
assess_model(dynmodel_men, time(tbts_men)[7:36], tb_men[7:36,])
##
## Time series regression with "ts" data:
## Start = 7, End = 36
##
## Call:
## dynlm(formula = ts(salary) ~ L(ts(salary), 6) - 1, data = tb_men,
## weights = n[7:36])
##
## Weighted Residuals:
## Min 1Q Median 3Q Max
## -165299 -8902 0 47573 133181
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## L(ts(salary), 6) 1.019380 0.002739 372.1 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 73750 on 22 degrees of freedom
## Multiple R-squared: 0.9998, Adjusted R-squared: 0.9998
## F-statistic: 1.385e+05 on 1 and 22 DF, p-value: < 2.2e-16
##
##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## L(ts(salary), 6) 1.0193798 0.0020172 505.35 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1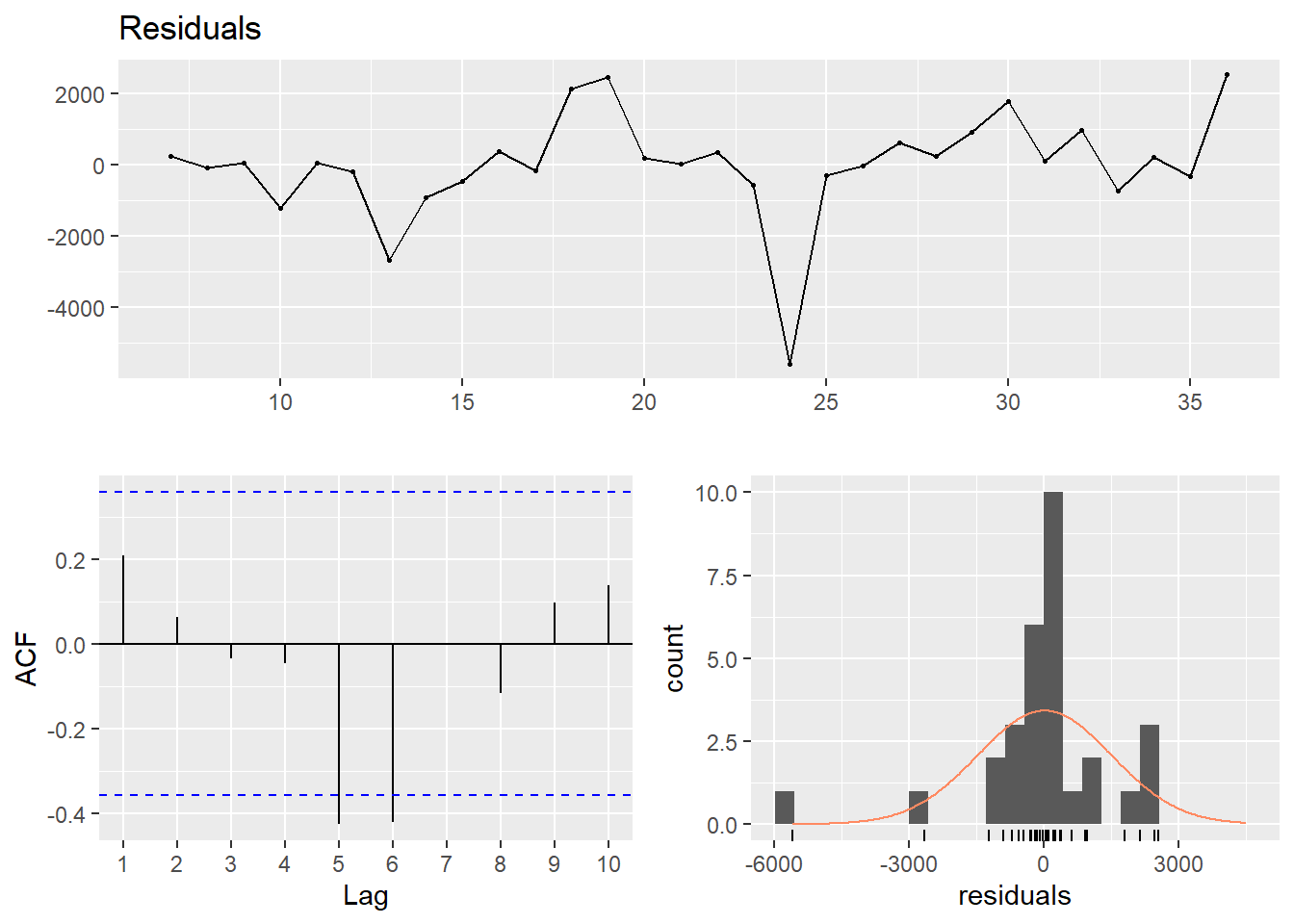
##
## Breusch-Godfrey test for serial correlation of order up to 6
##
## data: Residuals
## LM test = 9.9529, df = 6, p-value = 0.1266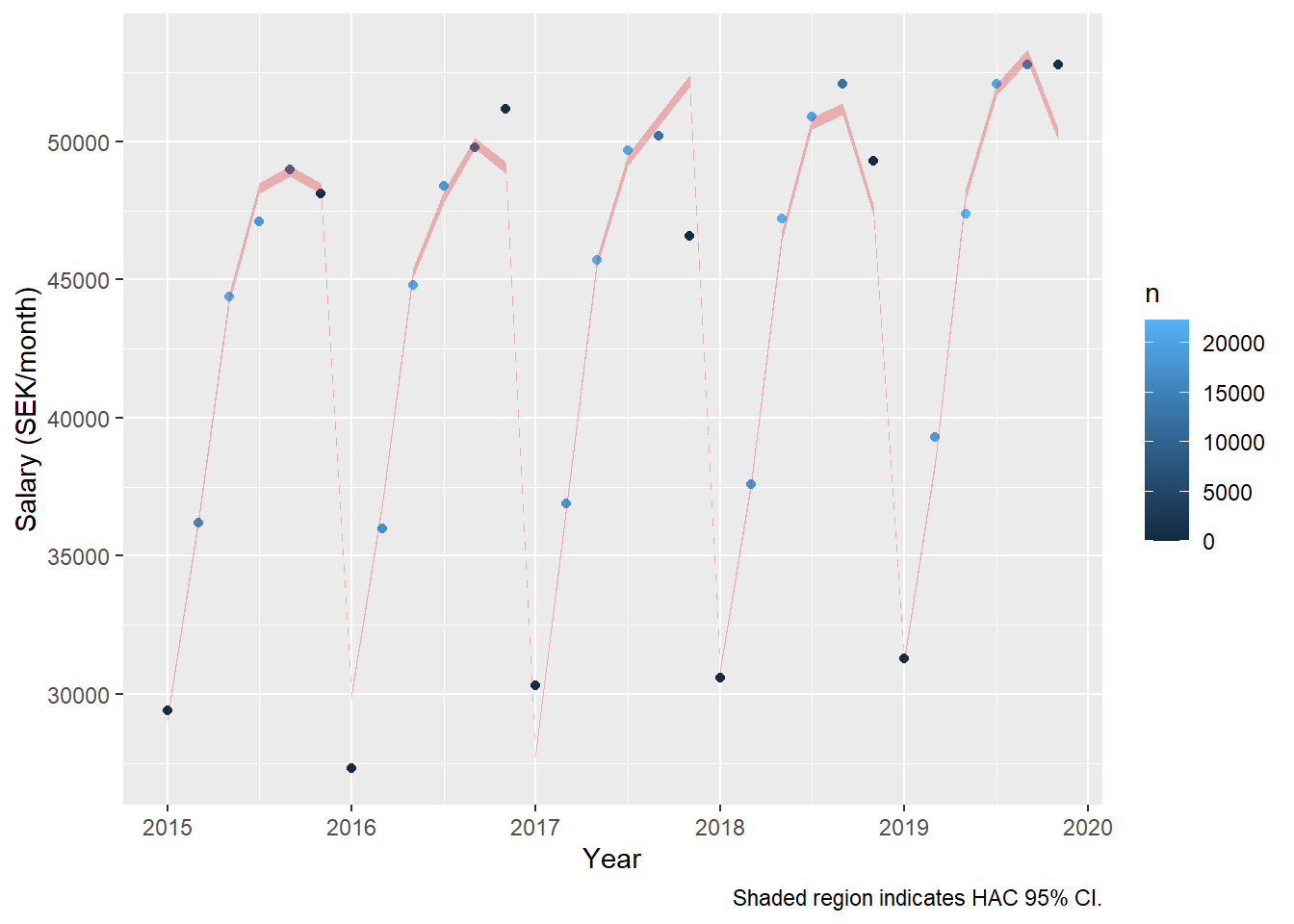
dynmodel_women <- dynlm(ts(salary) ~ L(ts(salary),5) - 1, data = tb_women, weights = n[6:30])
assess_model(dynmodel_women, time(tbts_women)[6:30], tb_women[6:30,])
##
## Time series regression with "ts" data:
## Start = 6, End = 30
##
## Call:
## dynlm(formula = ts(salary) ~ L(ts(salary), 5) - 1, data = tb_women,
## weights = n[6:30])
##
## Weighted Residuals:
## Min 1Q Median 3Q Max
## -103209 -32580 0 36088 146345
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## L(ts(salary), 5) 1.020343 0.004217 241.9 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 59020 on 22 degrees of freedom
## Multiple R-squared: 0.9996, Adjusted R-squared: 0.9996
## F-statistic: 5.853e+04 on 1 and 22 DF, p-value: < 2.2e-16
##
##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## L(ts(salary), 5) 1.0203429 0.0035569 286.86 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1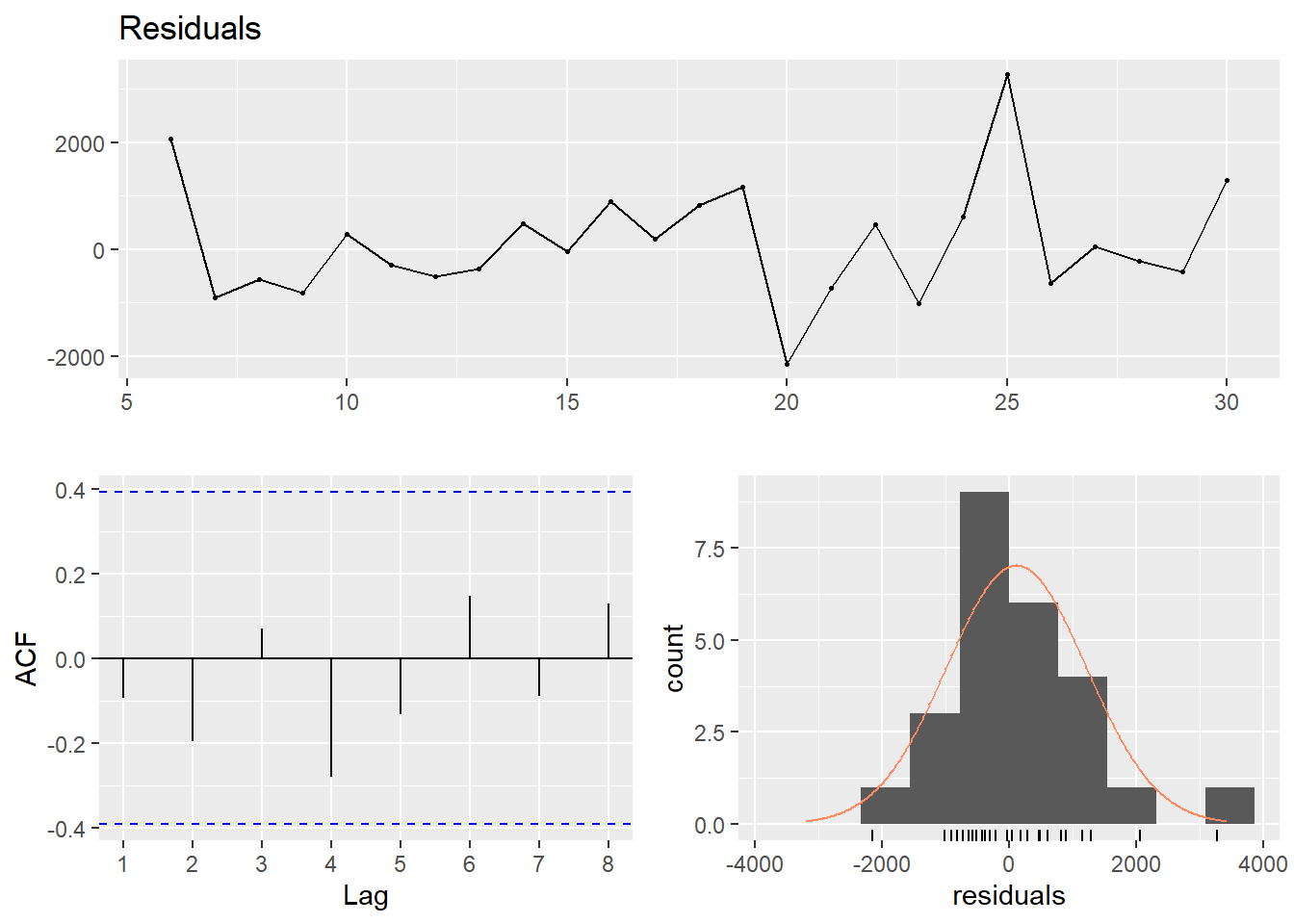
##
## Breusch-Godfrey test for serial correlation of order up to 5
##
## data: Residuals
## LM test = 4.9459, df = 5, p-value = 0.4225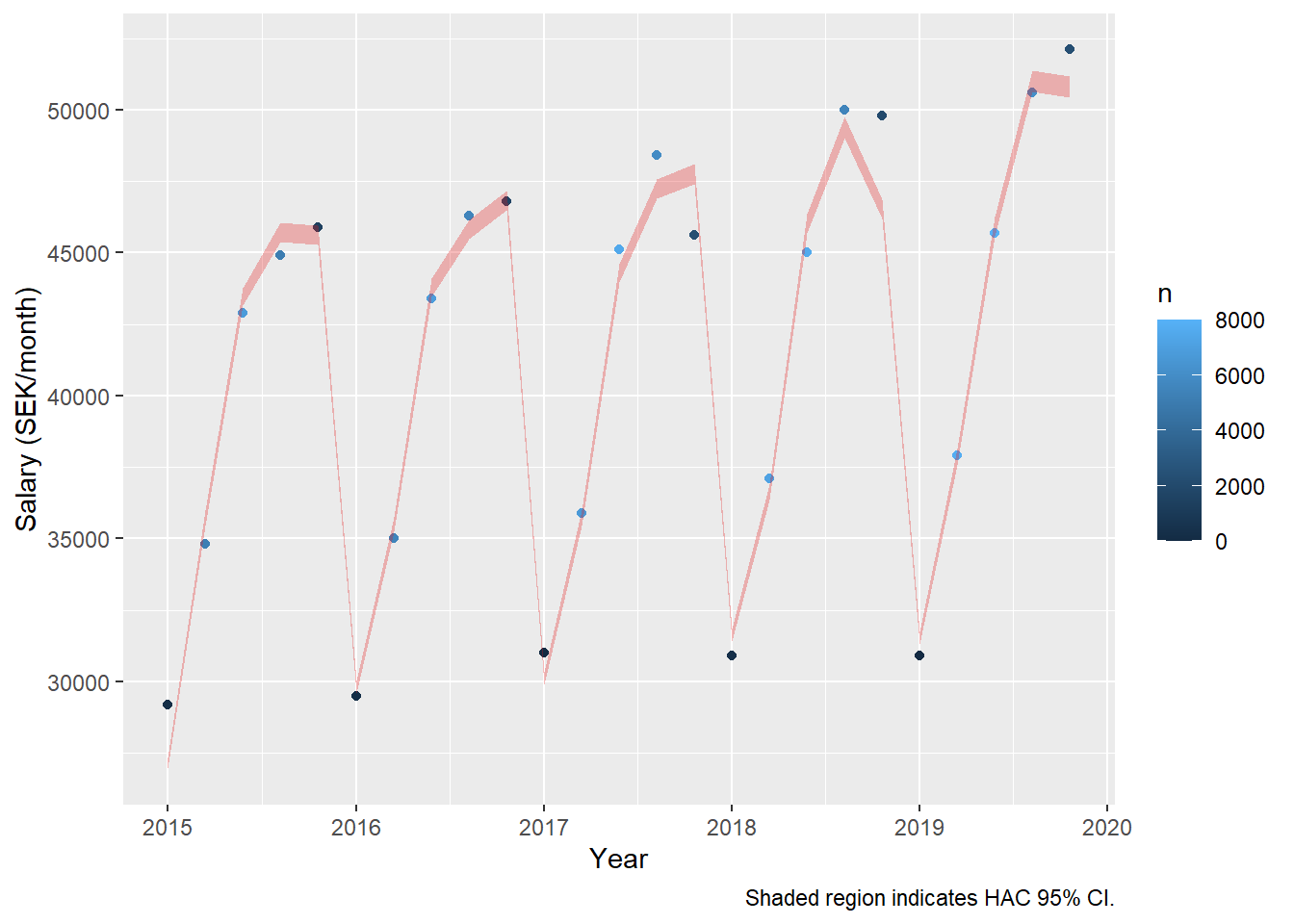
Now, let’s compare with a linear model. The relative salary raise increases to 1,92 % per year for men and 2.06 % for women.
model_men <- lm(log(salary) ~ year_n + age_n + I(age_n^2), data = tb_men, weights = n)
assess_model(model_men, time(tbts_men), tb_men, doexp = TRUE)
##
## Call:
## lm(formula = log(salary) ~ year_n + age_n + I(age_n^2), data = tb_men,
## weights = n)
##
## Weighted Residuals:
## Min 1Q Median 3Q Max
## -3.5386 -0.1234 0.0000 0.7387 2.7634
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -2.925e+01 3.086e+00 -9.479 2.08e-09 ***
## year_n 1.917e-02 1.530e-03 12.534 9.23e-12 ***
## age_n 5.160e-02 2.286e-03 22.569 < 2e-16 ***
## I(age_n^2) -4.670e-04 2.581e-05 -18.094 4.24e-15 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.694 on 23 degrees of freedom
## Multiple R-squared: 0.9898, Adjusted R-squared: 0.9885
## F-statistic: 746.4 on 3 and 23 DF, p-value: < 2.2e-16
##
##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -2.9252e+01 1.8119e+00 -16.145 4.852e-14 ***
## year_n 1.9171e-02 9.0239e-04 21.244 < 2.2e-16 ***
## age_n 5.1595e-02 1.6460e-03 31.347 < 2.2e-16 ***
## I(age_n^2) -4.6705e-04 1.7897e-05 -26.097 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1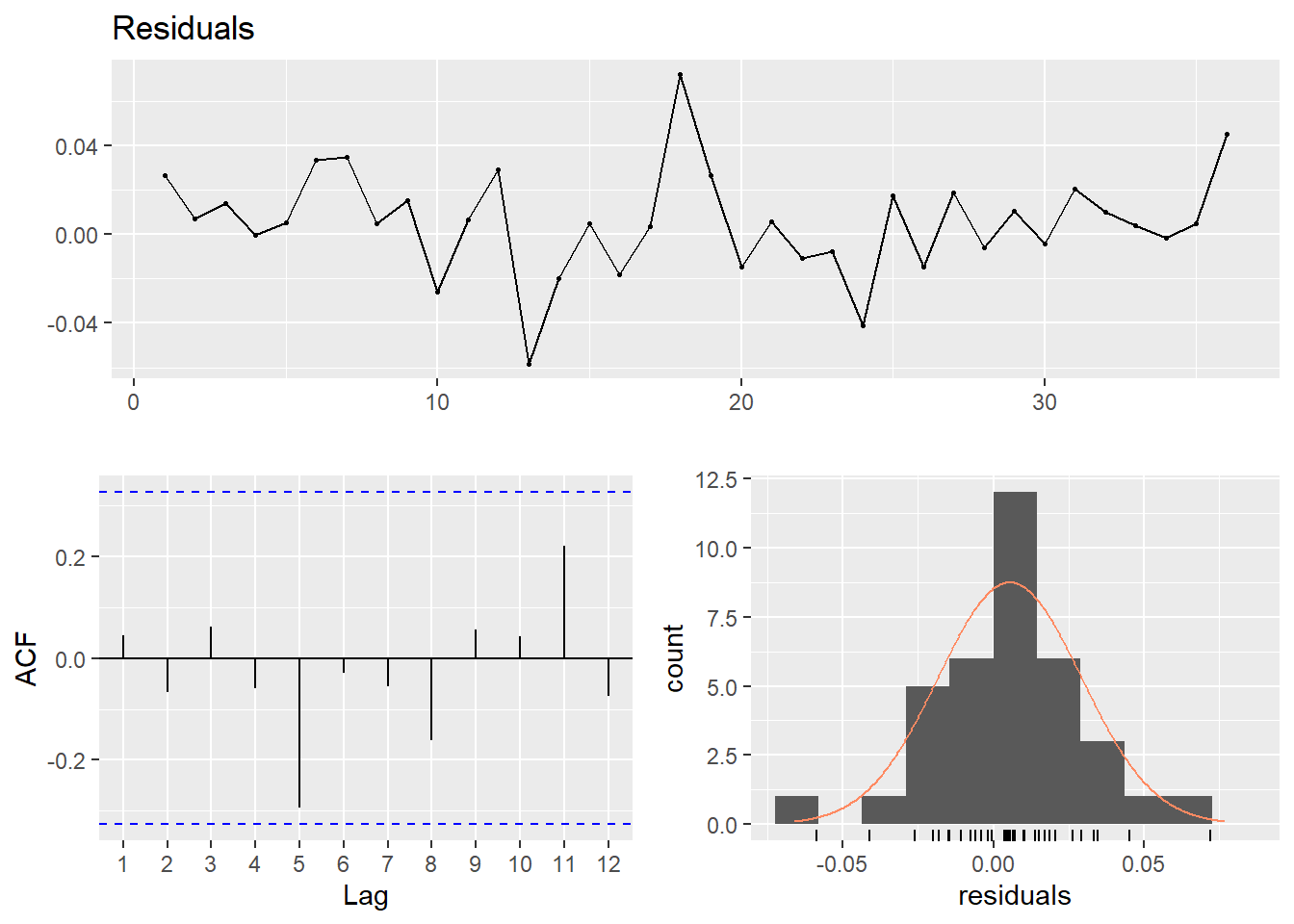
##
## Breusch-Godfrey test for serial correlation of order up to 7
##
## data: Residuals
## LM test = 6.7232, df = 7, p-value = 0.4583
## Don't know how to automatically pick scale for object of type ts. Defaulting to continuous.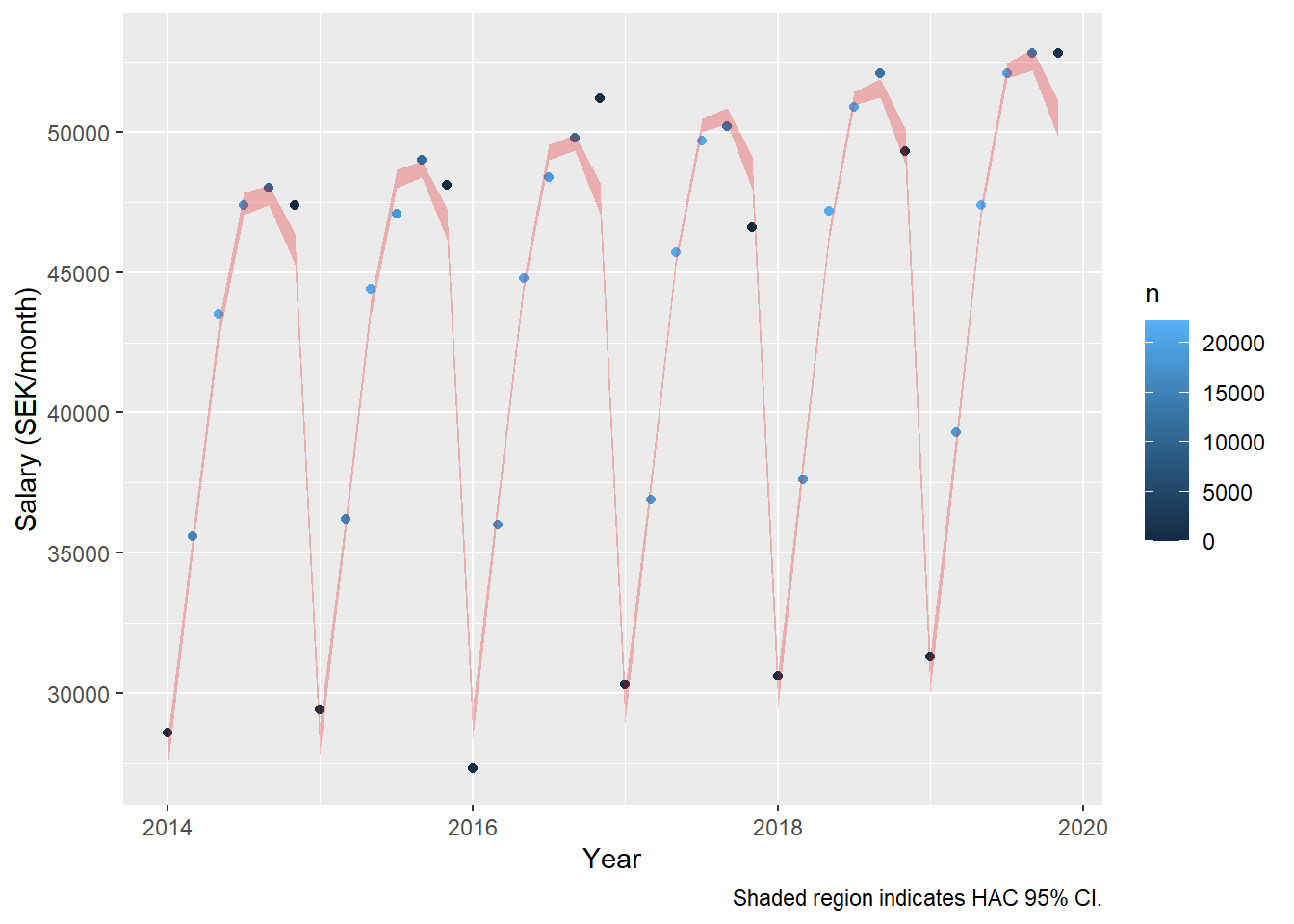
model_women <- lm(log(salary) ~ year_n + age_n + I(age_n^2), data = tb_women, weights = n)
assess_model(model_women, time(tbts_women), tb_women, doexp = TRUE)
##
## Call:
## lm(formula = log(salary) ~ year_n + age_n + I(age_n^2), data = tb_women,
## weights = n)
##
## Weighted Residuals:
## Min 1Q Median 3Q Max
## -2.31829 -0.34720 0.05136 0.89951 2.33846
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -3.228e+01 4.347e+00 -7.427 1.50e-07 ***
## year_n 2.063e-02 2.154e-03 9.580 1.71e-09 ***
## age_n 5.521e-02 3.330e-03 16.577 2.77e-14 ***
## I(age_n^2) -5.202e-04 3.912e-05 -13.298 2.77e-12 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.288 on 23 degrees of freedom
## Multiple R-squared: 0.9798, Adjusted R-squared: 0.9771
## F-statistic: 371.4 on 3 and 23 DF, p-value: < 2.2e-16
##
##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -3.2285e+01 3.9562e+00 -8.1605 3.045e-08 ***
## year_n 2.0631e-02 1.9667e-03 10.4903 3.075e-10 ***
## age_n 5.5206e-02 2.7439e-03 20.1196 4.246e-16 ***
## I(age_n^2) -5.2025e-04 3.3832e-05 -15.3777 1.357e-13 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1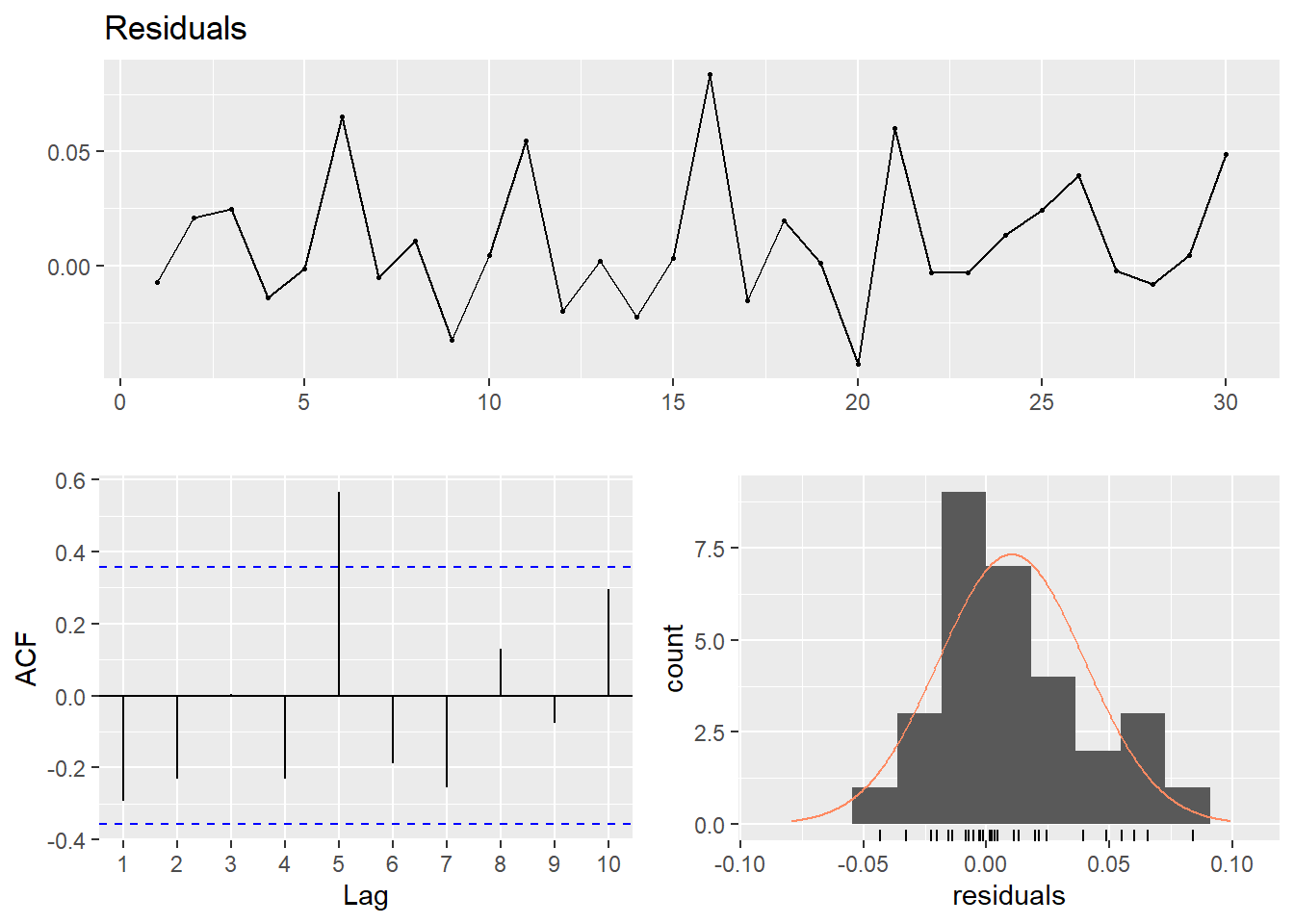
##
## Breusch-Godfrey test for serial correlation of order up to 7
##
## data: Residuals
## LM test = 11.678, df = 7, p-value = 0.1117
## Don't know how to automatically pick scale for object of type ts. Defaulting to continuous.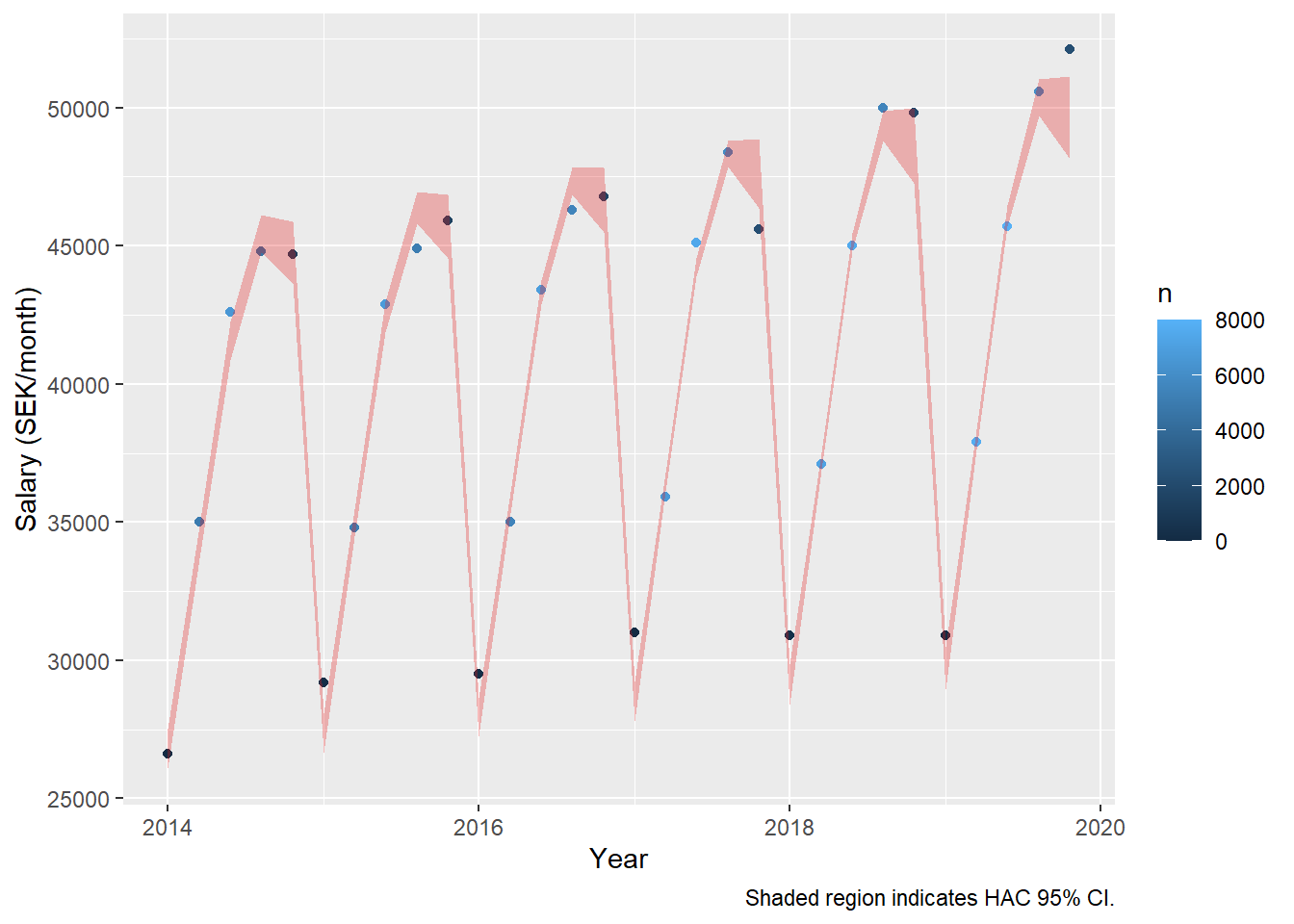
Now also add the SAR(2). The summary shows that the R-squared bumps up a few notches for men, although it does not show that the second year lag is significant. However, the sandwich package assures us that the SAR(2) process is significant at the 95 % level. For women, the second year lag is not significant in the summary nor the HAC error estimate.
dynmodel_men <- dynlm(ts(salary) ~ L(ts(salary), 6) + L(ts(salary), 12) - 1, data = tb_men, weights = n[13:36])
assess_model(dynmodel_men, time(tbts_men)[13:36], tb_men[13:36,])
##
## Time series regression with "ts" data:
## Start = 13, End = 36
##
## Call:
## dynlm(formula = ts(salary) ~ L(ts(salary), 6) + L(ts(salary),
## 12) - 1, data = tb_men, weights = n[13:36])
##
## Weighted Residuals:
## Min 1Q Median 3Q Max
## -127942 -17989 0 42788 123721
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## L(ts(salary), 6) 0.7282 0.2371 3.071 0.00692 **
## L(ts(salary), 12) 0.2985 0.2417 1.235 0.23356
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 69840 on 17 degrees of freedom
## Multiple R-squared: 0.9999, Adjusted R-squared: 0.9999
## F-statistic: 6.4e+04 on 2 and 17 DF, p-value: < 2.2e-16
##
##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## L(ts(salary), 6) 0.72822 0.11497 6.3338 7.484e-06 ***
## L(ts(salary), 12) 0.29855 0.11741 2.5427 0.02102 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1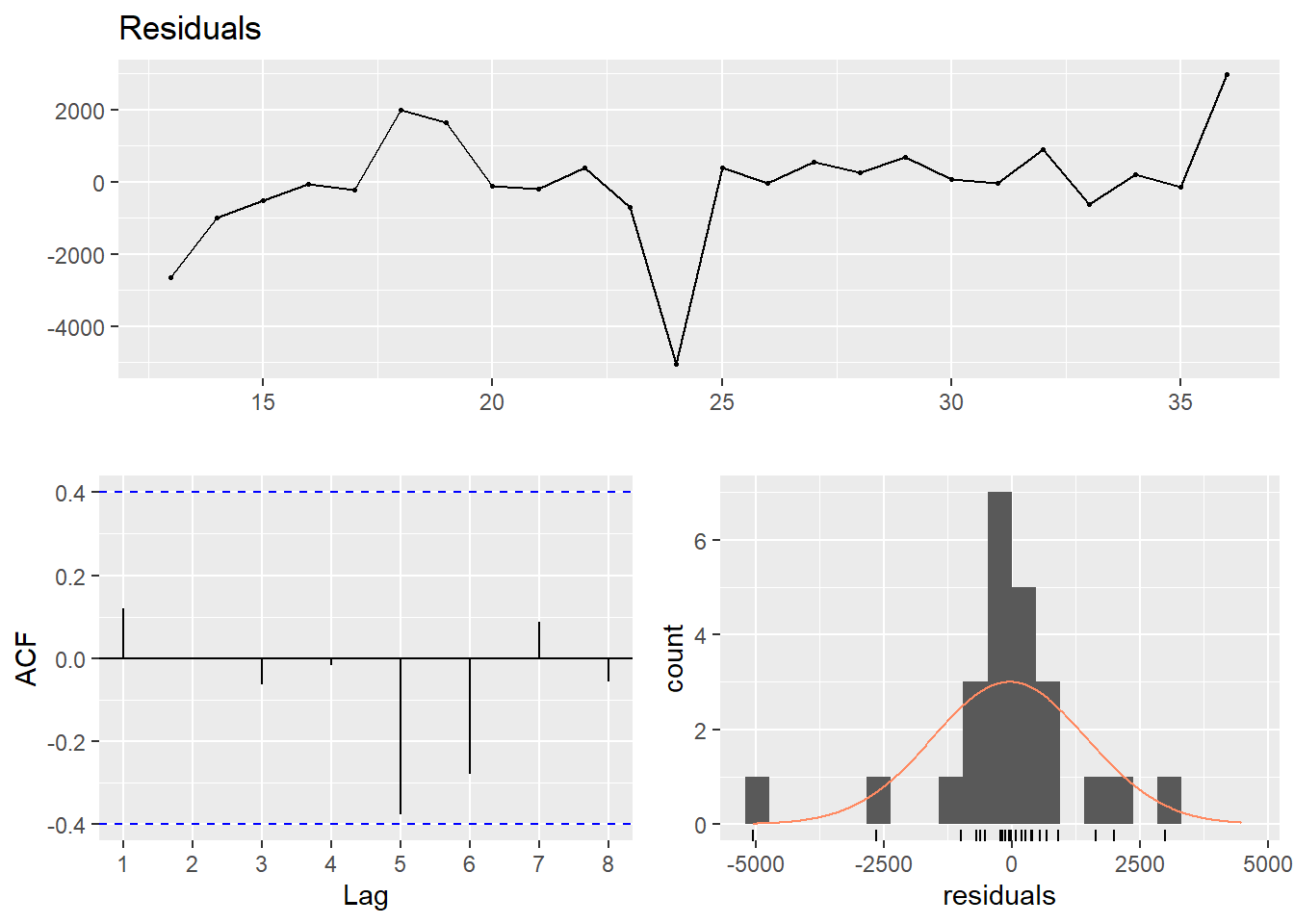
##
## Breusch-Godfrey test for serial correlation of order up to 5
##
## data: Residuals
## LM test = 3.9255, df = 5, p-value = 0.5602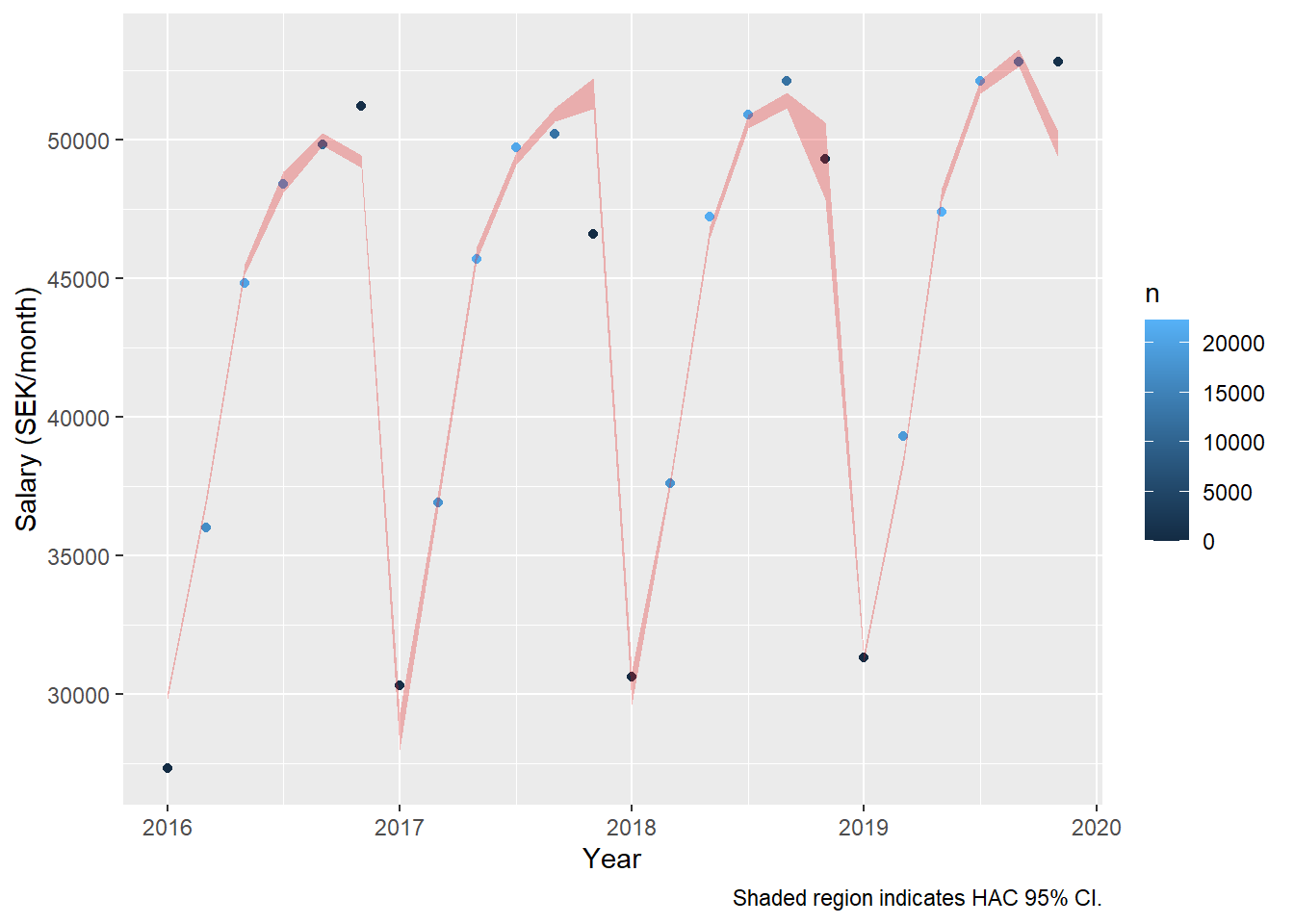
dynmodel_women <- dynlm(ts(salary) ~ L(ts(salary), 5) + L(ts(salary), 10) - 1, data = tb_women, weights = n[11:30])
summary (dynmodel_women)
##
## Time series regression with "ts" data:
## Start = 11, End = 30
##
## Call:
## dynlm(formula = ts(salary) ~ L(ts(salary), 5) + L(ts(salary),
## 10) - 1, data = tb_women, weights = n[11:30])
##
## Weighted Residuals:
## Min 1Q Median 3Q Max
## -110096 -37862 -1787 33549 134747
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## L(ts(salary), 5) 0.96703 0.23193 4.169 0.000723 ***
## L(ts(salary), 10) 0.05749 0.23683 0.243 0.811298
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 63340 on 16 degrees of freedom
## Multiple R-squared: 0.9996, Adjusted R-squared: 0.9996
## F-statistic: 2.14e+04 on 2 and 16 DF, p-value: < 2.2e-16
coeftest(dynmodel_women, vcov = NeweyWest, prewhite = F, adjust = T)
##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## L(ts(salary), 5) 0.967032 0.122156 7.9164 6.354e-07 ***
## L(ts(salary), 10) 0.057485 0.125308 0.4588 0.6526
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1